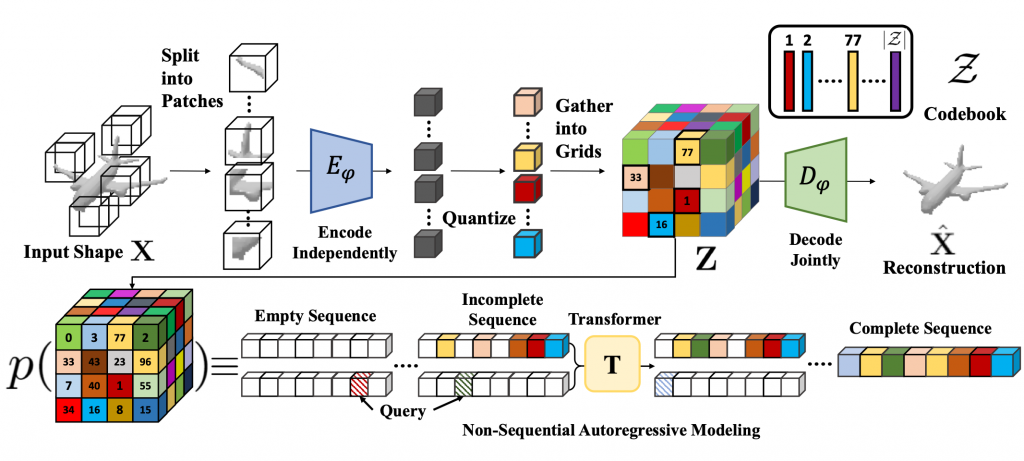
Discretized Latent Space for 3D Shapes
To learn an effective autoregressive model, we aim to reduce the high-dimensional continuous 3D shape representation to a lower-dimensional discrete latent space. Towards this, we adapt the VQ-VAE [1] framework and learn a 3D-VQ-VAE whose encoder Eψ can compute the desired low-dimensional representation, and the decoder Dψ can map this latent space back to/ 3D shapes. Given a 3D shape X with spatial dimension of D3 we have
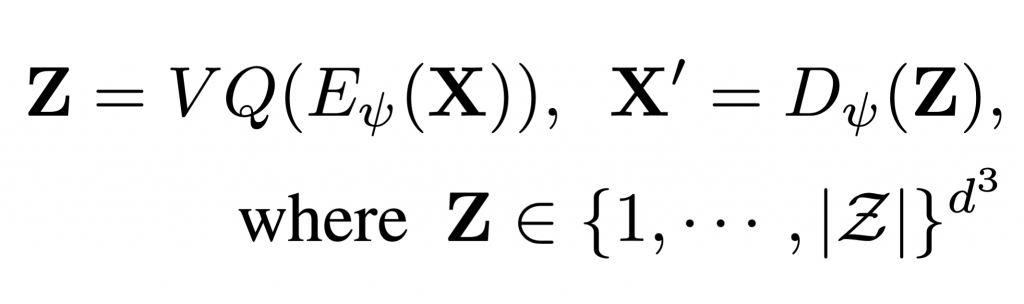
where VQ is the Vector Quantization step that maps a vector to the nearest element in the codebook. The encoder Eψ has a very large receptive field. Unfortunately, this is not a desirable property for tasks such as shape completion since the latent codes for encoded partial shapes may differ significantly from those of the encoded full shape — thus partial observations of shape may not correspond to partial observations of latent variables. To overcome this challenge, we propose Patch-wise Encoding VQ-VAE or P-VQ-VAE that encodes the local shape regions independently, while decoding them jointly — this allows the discrete encodings to only depend on local context.
Non-sequential Autoregressive Modeling
The latent space Z is a 3D grid of tokens representing the original 3D shape. We can thus reduce the task of learning the distribution over continuous 3D shapes to learning p(Z). An autoregressive model like transformer can model this distribution by factoring it as a product of location specific conditionals. However, this factorization assumes a fixed ordering in which the tokens are observed/generated. This is generally not true for conditioning tasks like shape completion, reconstruction etc. We follow the observation from [2] that the joint distribution p(Z) can be factorized into terms of the form p(zi| O), where O is a random set of observed variables. Hence we use a randomly permuted sequence of latent variables {zg1, zg2, zg3, …} for autoregressively modeling the distribution p(z):
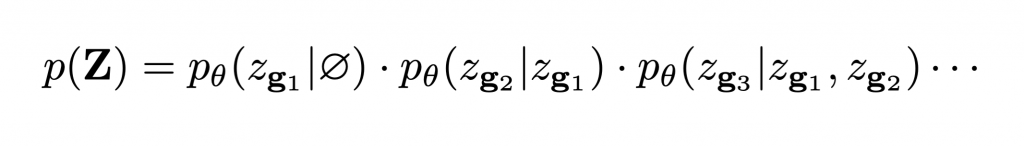
The non-sequential autoregressive network models the distribution over the latent variables Z, which can be mapped to full 3D shapes X = Dψ(Z)
Conditional Generation
- Shape Completion: The proposed P-VQ-VAE encodes local regions independently. This enables us to map partially observed shape Xp to corresponding observed latent variables O = {zg1, zg2, …., zgk}. In particular, we can formulate the task of shape completion as:
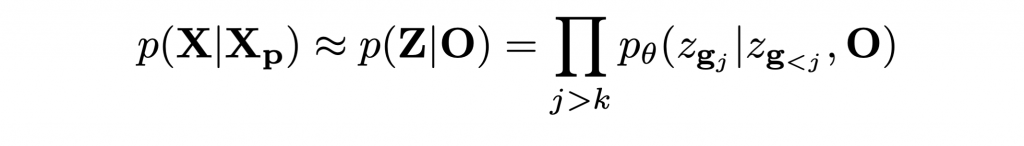
Based on the above formulation, we can directly use our model to autoregressively sample complete latent codes from partial observations.
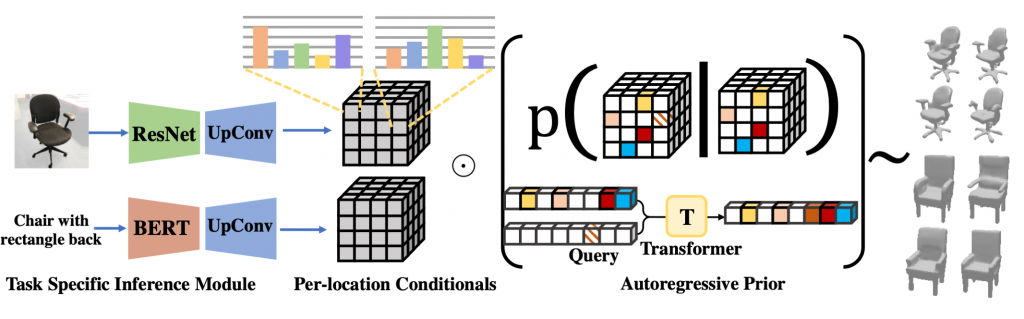
- Approximating generic conditional distributions: In this project we propose to model the distribution p(Z | C) as a product of the shape prior, coupled with independent ‘naive’ conditional terms that weakly capture the dependence on the conditioning C:
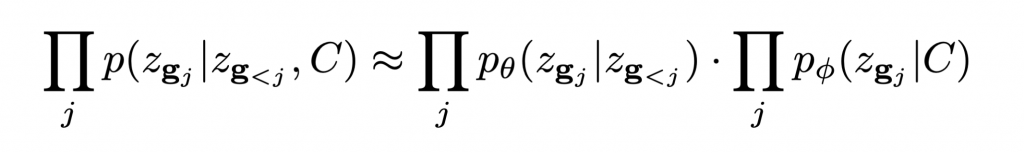
This factorization corresponds to assuming a factor graph where the conditioning C is connected to each latent variable zi with only a pairwise potential p(zi|C).
- Learning Naive Conditionals: For this project, we train task-specific networks comprising of domain specific encoders (e.g. ResNet for images, BERT for language etc.) fine-tuned on limited paired data (X, C). Each conditional is trained to predict the conditional distribution over elements in Z as explained in fig. 2. During inference we sample from a combination of the two distributions (per-location conditionals and shape prior) for generating a complete latent sequence.
References
[1] Aaron van den Oord, Oriol Vinyals, and Koray Kavukcuoglu. Neural discrete representation learning. In NeurIPS, 2017.
[2] Shubham Tulsiani and Abhinav Gupta. Pixeltransformer: Sample conditioned signal generation. In ICML, 202