Motivation

3D representations are essential for applications in robotics, self-driving, virtual/augmented reality, and online marketplaces. This has led to an increasing number of diverse tasks that rely on effective 3D representations — a robot might need to predict the shape of the objects it encounters, an artist may want to imagine what a ‘thin couch’ would look like, or a woodworker may want to explore possible tabletop designs to match the legs they carved. A common practice for tackling these tasks, such as 3D completion or single-view prediction is to utilize task-specific data and train individual systems for each task, requiring a large amount of compute and data resources.

Our capstone is motivated by the observation that a generalized notion of what ‘tables’ are is useful for both predicting the full shape from the left half and imagining what ‘a tall round table’ may look like. In this work, we operationalize this observation and show that a generic shape prior can be leveraged across different inference tasks.

Our approach combines a non-sequential autoregressive prior for 3D shapes with task-specific conditionals to generate multiple plausible and high-quality shapes consistent with input conditioning. We show the efficacy of our approach across diverse tasks such as (Left) **shape completion**, (Middle) **single-view reconstruction** and (Right) **language-guided generation**.

Introduction

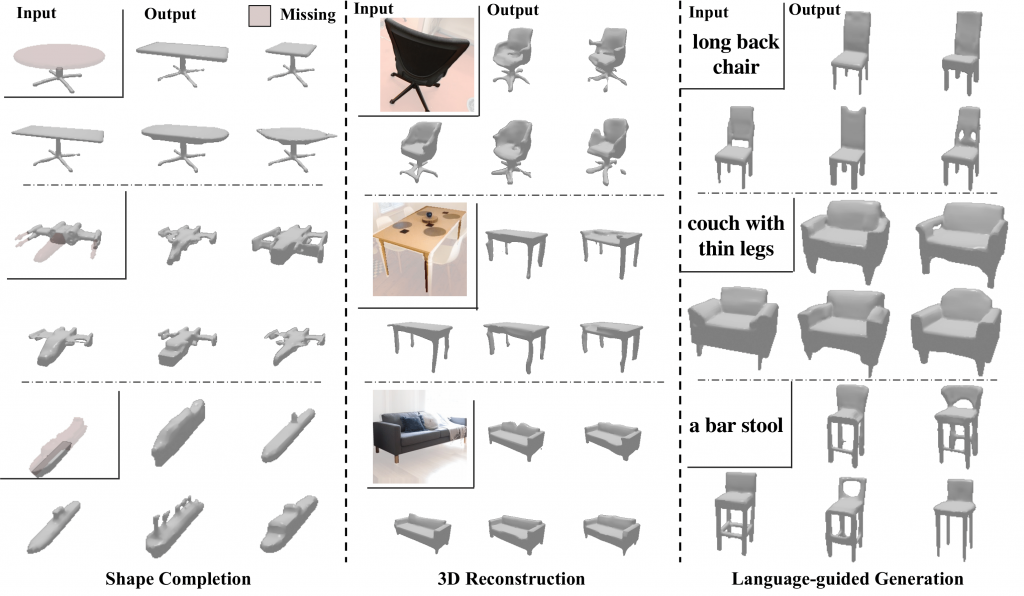
Plethora of problems in computer vision can be grouped under the umbrella of conditional generation. For this project, we primarily focus on the tasks of 3D shape completion, image and language guided 3D shape generations etc. While these tasks are seemingly different, they require similar outputs — a distribution over the plausible 3D structure conditioned on the corresponding input. This work is hence aimed at learning an expressive autoregressive shape prior from abundantly available raw 3D data. This prior can then help augment the task-specific conditional distributions which require paired training data (e.g. language-shape pairs), and significantly improve performance when such paired data is difficult to acquire.

We then present a common framework for leveraging our learned prior for conditional generation tasks e.g. single-view reconstruction or language-guided generation. Instead of modeling the complex conditional distribution directly, we propose to approximate it as a product of the prior and task-specific conditionals, the latter of which can be learned without extensive training data. Combined with the rich and expressive shape prior, we find that this unified and simple approach leads to improvements over task-specific state-of-the methods.

Contributions

Key contributions of this work include:

Developing a method to map continuous and high-dimensional space of 3D shapes to a discretized and low-dimensional representations for 3D shapes.
Learning a self-supervised non-sequential autoregressive 3D shape prior
Proposing a common framework for leveraging our learned prior for conditional generation tasks using pre-trained domain specific encoders.