Survey Presentation
Mid term Presentation
Fall-21 Final Capstone Presentation [slides] [video]
Current Results
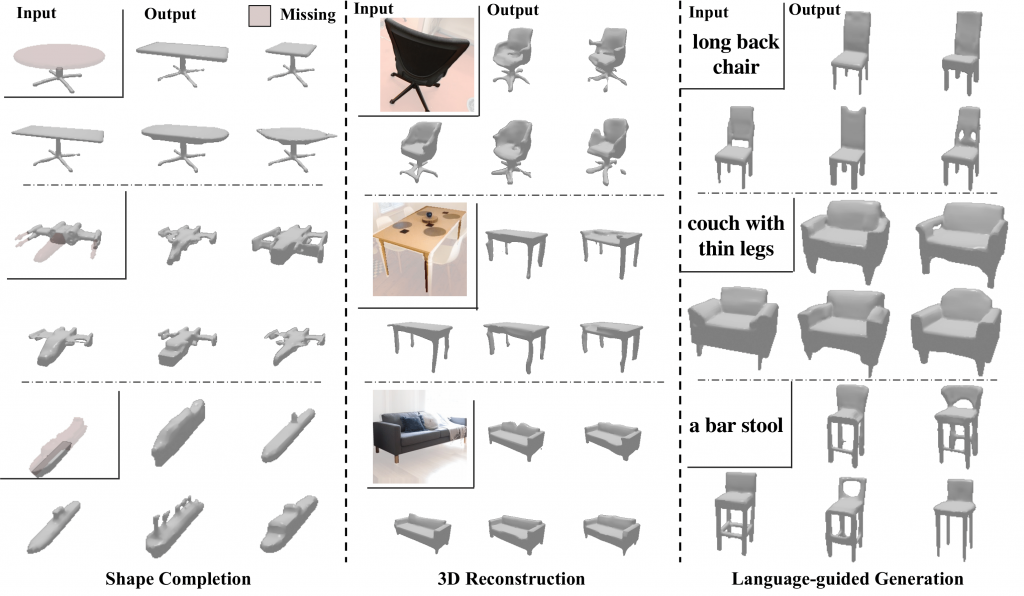
Qualitative Comparisons for Shape Completion
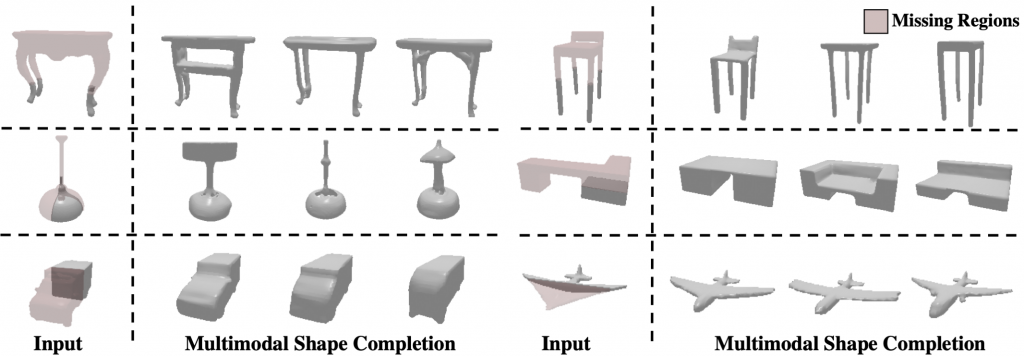
Qualitative Comparisons for Single View Reconstruction

Qualitative Comparisons for Language based Generations
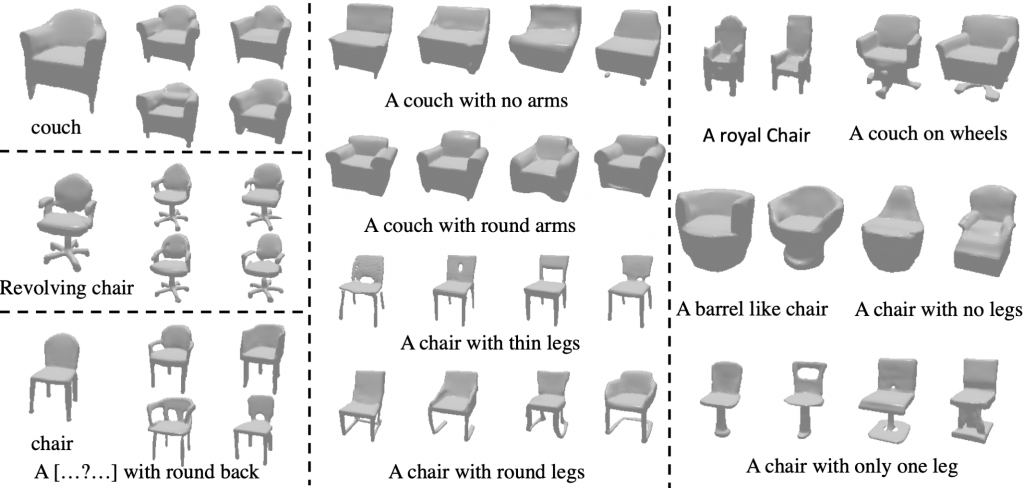
For more of our amazing results please visit here.
Approach
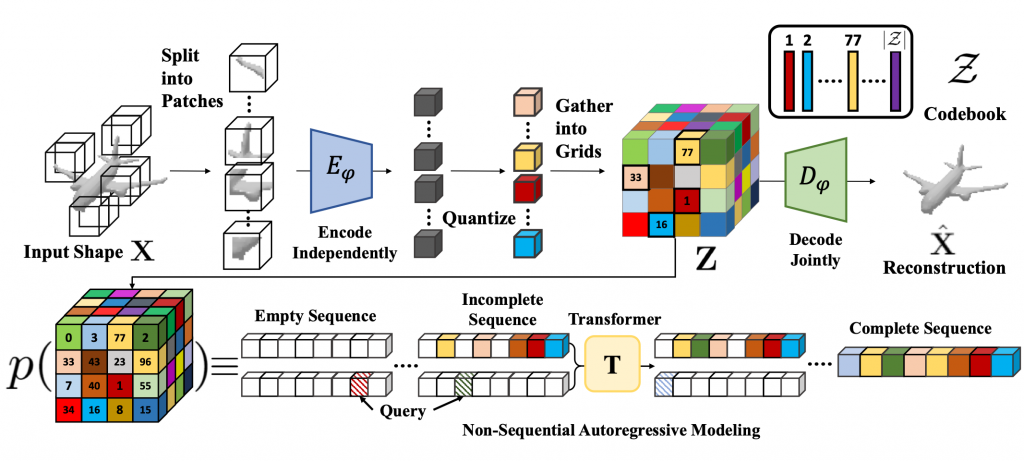
Discretized Latent Space for 3D Shapes
To learn an effective autoregressive model, we aim to reduce the high-dimensional continuous 3D shape representation to a lower-dimensional discrete latent space. Towards this, we adapt the VQ-VAE [1] framework and learn a 3D-VQ-VAE whose encoder Eψ can compute the desired low-dimensional representation, and the decoder Dψ can map this latent space back to/ 3D shapes. Given a 3D shape X with spatial dimension of D3 we have
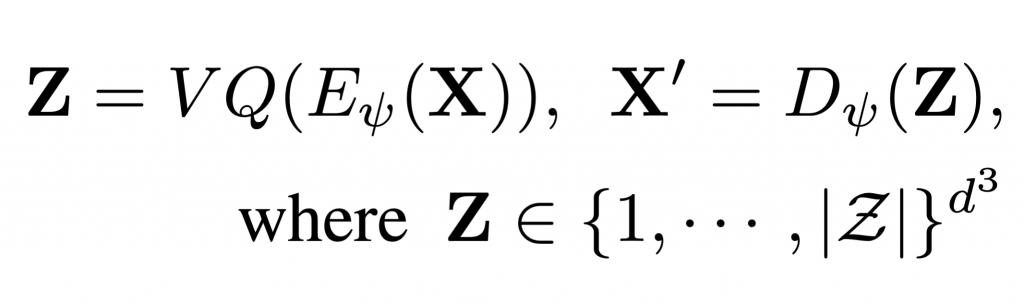
where VQ is the Vector Quantization step that maps a vector to the nearest element in the codebook. The encoder Eψ has a very large receptive field. Unfortunately, this is not a desirable property for tasks such as shape completion since the latent codes for encoded partial shapes may differ significantly from those of the encoded full shape — thus partial observations of shape may not correspond to partial observations of latent variables. To overcome this challenge, we propose Patch-wise Encoding VQ-VAE or P-VQ-VAE that encodes the local shape regions independently, while decoding them jointly — this allows the discrete encodings to only depend on local context.
Non-sequential Autoregressive Modeling
The latent space Z is a 3D grid of tokens representing the original 3D shape. We can thus reduce the task of learning the distribution over continuous 3D shapes to learning p(Z). An autoregressive model like transformer can model this distribution by factoring it as a product of location specific conditionals. However, this factorization assumes a fixed ordering in which the tokens are observed/generated. This is generally not true for conditioning tasks like shape completion, reconstruction etc. We follow the observation from [2] that the joint distribution p(Z) can be factorized into terms of the form p(zi| O), where O is a random set of observed variables. Hence we use a randomly permuted sequence of latent variables {zg1, zg2, zg3, …} for autoregressively modeling the distribution p(z):
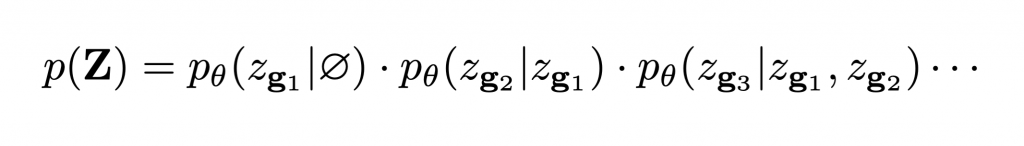
The non-sequential autoregressive network models the distribution over the latent variables Z, which can be mapped to full 3D shapes X = Dψ(Z)
Conditional Generation
- Shape Completion: The proposed P-VQ-VAE encodes local regions independently. This enables us to map partially observed shape Xp to corresponding observed latent variables O = {zg1, zg2, …., zgk}. In particular, we can formulate the task of shape completion as:
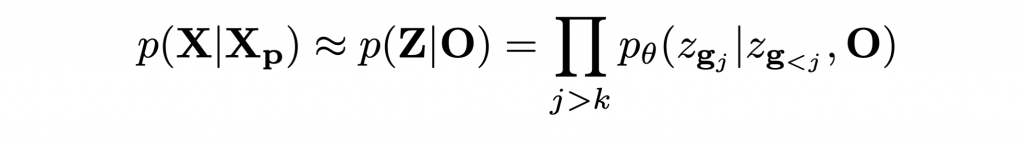
Based on the above formulation, we can directly use our model to autoregressively sample complete latent codes from partial observations.
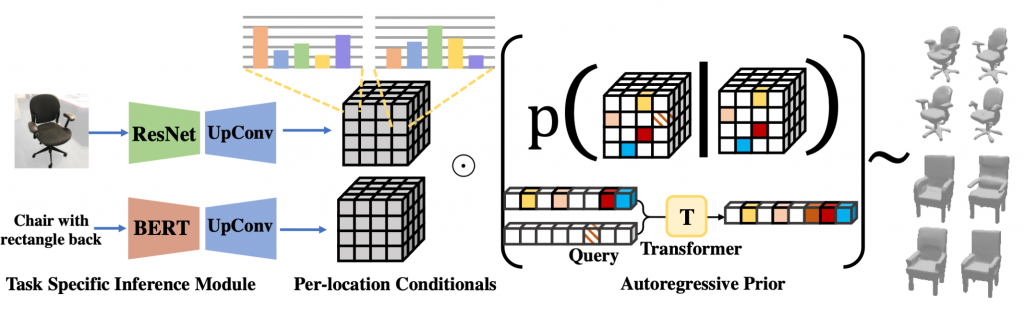
- Approximating generic conditional distributions: In this project we propose to model the distribution p(Z | C) as a product of the shape prior, coupled with independent ‘naive’ conditional terms that weakly capture the dependence on the conditioning C:
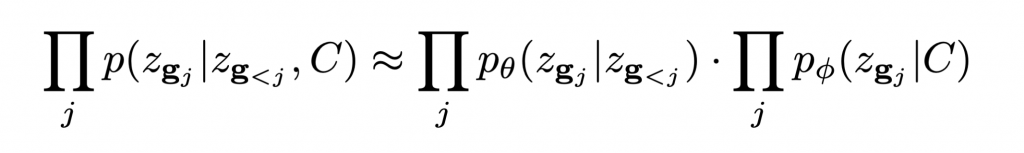
This factorization corresponds to assuming a factor graph where the conditioning C is connected to each latent variable zi with only a pairwise potential p(zi|C).
- Learning Naive Conditionals: For this project, we train task-specific networks comprising of domain specific encoders (e.g. ResNet for images, BERT for language etc.) fine-tuned on limited paired data (X, C). Each conditional is trained to predict the conditional distribution over elements in Z as explained in fig. 2. During inference we sample from a combination of the two distributions (per-location conditionals and shape prior) for generating a complete latent sequence.
References
[1] Aaron van den Oord, Oriol Vinyals, and Koray Kavukcuoglu. Neural discrete representation learning. In NeurIPS, 2017.
[2] Shubham Tulsiani and Abhinav Gupta. Pixeltransformer: Sample conditioned signal generation. In ICML, 202
Related Work
Autoregressive modeling
Autoregressive models [12] factorize the joint distribution over structured outputs into products of conditional distribution. Unlike GANs [9], these can serve as powerful density estimators [14], are more stable during training [13,14], and can generalize well on held-out data. They have been successfully leveraged for modeling distributions across domains, such as images[5,12,13], video, or language [16], and our work explores their benefits across a broad range of 3D generation tasks.
Following their recent successes in autoregressive modeling[3,16] our work adapts a Transformer-based [17] architecture. However, these approaches cannot directly be adopted to volumetric 3D representations due to their high resolutions. We build on the work by van den Oord et.al. [15] who proposed a method to learn quantized and compact latent representations for images using Vector-Quantized Variational AutoEncoder (VQ-VAE). Inspired by Esser et.al. [7] who learned autoregressive generation over the discrete VQ-VAE representations, our work extends these ideas to the domain of 3D shapes.
Shape Completion
Completing full shapes from partial inputs such as discrete parts, or single-view 3D, is an increasingly important task across robotics and graphics. Most recent approaches [1,4,18] formulate it as performing completion on point clouds and can infer plausible global shapes but have difficulty in either capturing fine-grained details, conditioning on sparse inputs, or generating diverse samples. Our work proposes an alternative approach using autoregressive shape priors.
Single View Reconstruction
Inferring the 3D shape from a single image is an inherently ill-posed task. Several approaches have shown impressive single-view reconstruction results using voxels [6,8], point clouds [11,19], and most recently implicit representations of 3D surfaces like SDFs [10,20] etc. However, these are often deterministic in nature and only generate a 3D single output. By treating image-based prediction as conditional distributions our work can capture the multi-modal aspect of conditional generation in a simple and elegant manner.
Language based Generation
Language is a highly effective and parsimonious modality for describing real world shapes and objects. Chen et.al [2] proposed a method to learn a joint text-shape embedding, followed by a GAN [9] based generator for synthesizing 3D from text. However, generating shapes from text is a fundamentally multi-modal task, and a GAN based approach struggles to capture the multiple output modes. In contrast, our project aims to first learn a ‘naive’ language guided conditional distribution and combine it with shape priors to generate diverse and plausible shapes.
References
[1] Panos Achlioptas, Olga Diamanti, Ioannis Mitliagkas, and Leonidas Guibas. Learning representations and generative models for 3d point clouds. In ICML, 2018.
[2] Kevin Chen, Christopher B Choy, Manolis Savva, Angel X Chang, Thomas Funkhouser, and Silvio Savarese. Text2shape: Generating shapes from natural language by learning joint embeddings. In ACCV, 2018.
[3] Mark Chen, Alec Radford, Rewon Child, Jeffrey Wu, Heewoo Jun, David Luan, and Ilya Sutskever. Generative pretraining from pixels. In ICML, 2020.
[4] Xuelin Chen, Baoquan Chen, and Niloy J Mitra. Unpaired point cloud completion on real scans using adversarial training. In ICLR, 2020.
[5] Xi Chen, Nikhil Mishra, Mostafa Rohaninejad, and Pieter Abbeel. Pixelsnail: An improved autoregressive generative model. In ICML, 2018
[6] Christopher B Choy, Danfei Xu, JunYoung Gwak, Kevin Chen, and Silvio Savarese. 3d-r2n2: A unified approach for single and multi-view 3d object reconstruction. In ECCV, 2016.
[7] Patrick Esser, Robin Rombach, and Bjorn Ommer. Taming transformers for high resolution image synthesis. In CVPR, 2021.
[8] Shubham Tulsiani, Tinghui Zhou, Alexei A. Efros, and Jitendra Malik. Multi-view supervision for single-view reconstruction via differentiable ray consistency. In CVPR,2017.
[9] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In NeurIPS, 2014.
[10] Yue Jiang, Dantong Ji, Zhizhong Han, and Matthias Zwicker. Sdfdiff: Differentiable rendering of signed distance fields for 3d shape optimization. In CVPR, 2020.
[11] Priyanka Mandikal, Navaneet K. L., Mayank Agarwal, and Venkatesh Babu Radhakrishnan. 3d-lmnet: Latent embedding matching for accurate and diverse 3d point cloud reconstruction from a single image. In BMVC, 2018
[12] Aaron Van Oord, Nal Kalchbrenner, and Koray Kavukcuoglu. Pixel recurrent neural networks. In ICML, 2016
[13] Tim Salimans, Andrej Karpathy, Xi Chen, and Diederik P. Kingma. Pixelcnn++: A pixelcnn implementation with discretized logistic mixture likelihood and other modifications. In ICLR, 2017
[14] Benigno Uria, Iain Murray, and Hugo Larochelle. Rnade: The real-valued neural autoregressive density-estimator. In NeurIPS, 2013.
[15] Aaron van den Oord, Oriol Vinyals, and Koray Kavukcuoglu. Neural discrete representation learning. In NeurIPS, 2017.
[16] Zhilin Yang, Zihang Dai, Yiming Yang, Jaime Carbonell, Russ R Salakhutdinov, and Quoc V Le. Xlnet: Generalized autoregressive pretraining for language understanding. NeurIPS, 2019.
[17] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS, 2017
[18] Linqi Zhou, Yilun Du, and Jiajun Wu. 3d shape generation and completion through point-voxel diffusion. In ICCV, 2021.
[19] Rundi Wu, Yixin Zhuang, Kai Xu, Hao Zhang, and Baoquan Chen. Pq-net: A generative part seq2seq network for 3d shapes. In CVPR, 2020.
[20] Qiangeng Xu, Weiyue Wang, Duygu Ceylan, Radomir Mech, and Ulrich Neumann. Disn: Deep implicit surface network for high-quality single-view 3d reconstruction. In NeurIPS, 2019.
Project Summary
Motivation
3D representations are essential for applications in robotics, self-driving, virtual/augmented reality, and online marketplaces. This has led to an increasing number of diverse tasks that rely on effective 3D representations — a robot might need to predict the shape of the objects it encounters, an artist may want to imagine what a ‘thin couch’ would look like, or a woodworker may want to explore possible tabletop designs to match the legs they carved. A common practice for tackling these tasks, such as 3D completion or single-view prediction is to utilize task-specific data and train individual systems for each task, requiring a large amount of compute and data resources.
Our capstone is motivated by the observation that a generalized notion of what ‘tables’ are is useful for both predicting the full shape from the left half and imagining what ‘a tall round table’ may look like. In this work, we operationalize this observation and show that a generic shape prior can be leveraged across different inference tasks.
Introduction
Plethora of problems in computer vision can be grouped under the umbrella of conditional generation. For this project, we primarily focus on the tasks of 3D shape completion, image and language guided 3D shape generations etc. While these tasks are seemingly different, they require similar outputs — a distribution over the plausible 3D structure conditioned on the corresponding input. This work is hence aimed at learning an expressive autoregressive shape prior from abundantly available raw 3D data. This prior can then help augment the task-specific conditional distributions which require paired training data (e.g. language-shape pairs), and significantly improve performance when such paired data is difficult to acquire.
We then present a common framework for leveraging our learned prior for conditional generation tasks e.g. single-view reconstruction or language-guided generation. Instead of modeling the complex conditional distribution directly, we propose to approximate it as a product of the prior and task-specific conditionals, the latter of which can be learned without extensive training data. Combined with the rich and expressive shape prior, we find that this unified and simple approach leads to improvements over task-specific state-of-the methods.
Contributions
Key contributions of this work include:
- Developing a method to map continuous and high-dimensional space of 3D shapes to a discretized and low-dimensional representations for 3D shapes.
- Learning a self-supervised non-sequential autoregressive 3D shape prior
- Proposing a common framework for leveraging our learned prior for conditional generation tasks using pre-trained domain specific encoders.