We train a deep learning model, BodyMAP, to jointly predict the body mesh ˆM (3D pose & body shape), along with the 3D applied pressure map P . Specifically, our model takes the individual’s gender g, the depth image d, and the 2D pressure image p as inputs. The depth image is captured by a depth camera situated above the bed, while the 2D pressure image is generated by a pressure sensing mattress system positioned beneath the individual. This arrangement captures complementary features regarding the body illustrated in the appendix Fig. 5, thereby enhancing the context available to the model for accurate predictions of both body mesh and pressure map.
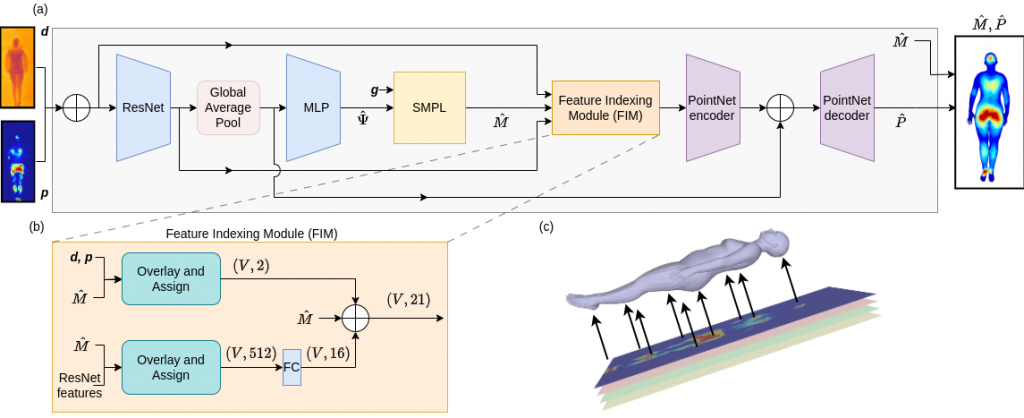
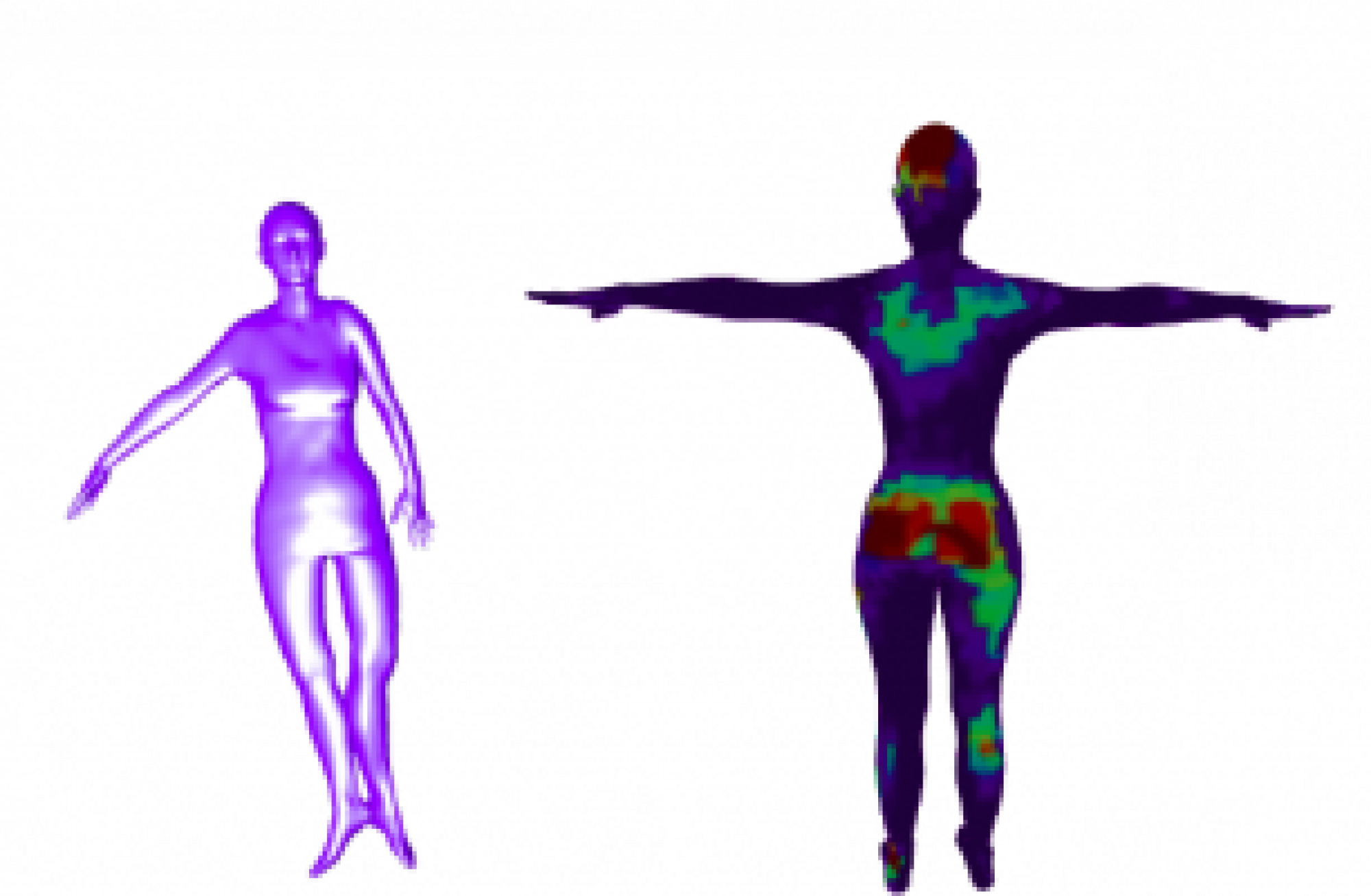
Figure 3: BodyMap jointly predicts body mesh and 3D applied pressure map for an individual in-bed. (a) Model architecture that encodes depth d and 2D pressure image p to predict SMPL [30] parameters ˆΨ, used to reconstruct the SMPL mesh ˆM . Feature Indexing Module (FIM) accumulates features for the mesh vertices from the input images and ResNet features. Finally, PointNet predicts the 3D pressure map ˆP along the human body using the mesh features as input. (b) FIM overlays the predicted mesh over the ResNet feature maps and input images by mapping mesh vertex locations to pixel positions and then assigns features for each vertex. These are fused along with the mesh vertex locations and used for 3D pressure map prediction. (c) Visualized FIM’s overlay and assign step.
Figure 3: The human body is represented using the SMPL [30] mesh, simplifying the network’s task to predict a handful of SMPL parameters for obtaining the mesh. A 3D pressure map is represented at the vertex level with a pressure value for each vertex of the human mesh, allowing for precise localization of high-pressure regions on the body. We train our models on both the BodyPressureSD dataset [9] of simulated humans in bed and the real-world SLP dataset [26, 28]. For both datasets, we have depth and pressure images, aligned with the 3D ground truth mesh for diverse poses (supine, left & right lateral) and multiple blanket thickness configurations.
BodyMAP
In this section, we detail the architecture of our model BodyMAP, as illustrated in Fig. 3. The depth and pressure images are resized, concatenated and processed together as
image channels by the model.
Body mesh prediction:
The input is first encoded using ResNet18 [15]. We then feed the latent features through
a multi-layer perceptron to predict the SMPL parameters ˆΨ. These parameters include body shape, joint angles, root joint translation, and root-joint rotation: ˆΨ = [ ˆβ, ˆΘ, ˆs, ˆx, ˆy].
The SMPL parameters ˆΨ, in addition to the gender information g, serve as inputs to the SMPL embedding block [19].
This block does not contain any learned parameters and outputs a differentiable human body mesh ˆM with vertices ˆV , and 3D joint positions ˆS.
Feature Indexing Module:
We introduce Feature Indexing Module (FIM), depicted in Fig. 3(b), to accumulate features for each mesh vertex. As mentioned in [9], the mesh predictions are spatially registered with the corresponding input images. This registration provides pixel locations where each mesh vertex would project onto the input images [9]. FIM assigns features to each mesh vertex from both the input images and the latent ResNet features (before global average pooling) using the mentioned pixel locations (Fig. 3(c)). These features are fused with the vertex locations and are utilized for pressure map prediction. Pressure map prediction: To predict a per-vertex pressure map ( ˆP ), we employ PointNet [37] utilizing the latent features formed from FIM for each vertex as input. This establishes a strong correlation between the mesh prediction and pressure prediction, ensuring their consistency with each other. In a manner akin to point-based segmentation architectures [37, 38], ResNet features (after global average pooling) are fused with PointNet encoder features. This provides the model with an enhanced contextual understanding. The PointNet decoder then predicts a per-vertex binary contact value and pressure value. The per-vertex contact value serves as an indicator of whether each mesh vertex is in contact with the mattress. We use the predicted contact values to further tune predicted pressure values. Specifically, the 3D pressure map is finally estimated as a product of the binary contact with the corresponding pressure value for each vertex.
Training strategy
We train the network to jointly predict body mesh and 3D applied pressure map with the following loss:
L = LSMPL + λ1Lv2v + λ2LP3D + λ3 Lcontact
where LSMPL minimizes the absolute error on SMPL parameters ˆΨ and squared error on the 3D joint positions ˆS. Lv2v (vertex-to-vertex loss) and LP3D minimize the squared error on the vertex positions and pressure map values respectively. Lcontact is applied as a cross entropy loss between predicted and ground truth 3D contact, where the ground truth 3D contact is obtained from all non-zero elements of the ground truth 3D pressure maps. The loss weighting coefficients are set empirically.
BodyMAP-WS
BodyMAP-WS is a variant of the above BodyMAP model, learning without supervision for the 3D pressure map prediction. This model utilizes a pre-trained mesh regressor to obtain mesh predictions and ResNet image features as its primary inputs. Unlike BodyMAP that forms the final 3D pressure map as the product of binary contact value and pressure at each vertex, to be able to train without supervision, BodyMAP-WS instead predicts only the pressure value at each vertex. The network architecture follows a similar design as BodyMAP’s pressure prediction part (Fig. 3) in its use of FIM and PointNet, and is further illustrated in the appendix Fig. 8. To facilitate learning of the accurate 3D pressure map, the model constructs a differentiable 2D projection of the predicted 3D pressure map by averaging the pressure values of the vertices that project to each pixel [9]. During training, the network aligns this 2D projection with the input pressure image, allowing for the implicit learning of the actual 3D applied pressure map onto the body mesh.
Training strategy
To form the pre-trained mesh regressor, we first train the mesh regressor section of BodyMAP using supervision with LSMPL and Lv2v. Subsequently, BodyMAP-WS is trained
to leverage the frozen pre-trained mesh model’s predicted ResNet features and mesh vertex locations as inputs, for predicting the 3D applied pressure map. This prediction is guided by the following loss function:
L = LP2D + λ1LPreg
Here, LPproj minimizes the squared error between the 2D projection of the predicted 3D pressure map and the input pressure image. The bed mattress is situated on the Z = 0 plane, and vertices predicted to be positioned above this plane (Z > 0) should ideally not have any applied pressure on them as they do not make contact with the mattress. To enforce this constraint, we utilize LPreg, a regularization term that penalizes for positive pressure on these vertices by minimizing the norm of predicted pressure values for these vertices.