TLDR: We model the HOI scene by a time-persistent implicit field for the object, hand meshes parameterized by hand shape, hand articulation, along with a time-varying rigid transformation for object pose. We define the cameras in the hand frame. We optimize a video-specific scene representation using reprojection loss from the original view and diffusion distillation loss from a novel view. Our diffusion model takes in a noisy geometry rendering of the object, the geometry rendering of the hand, and a text prompt, to output the denoised geometry rendering of objects.
Overview:
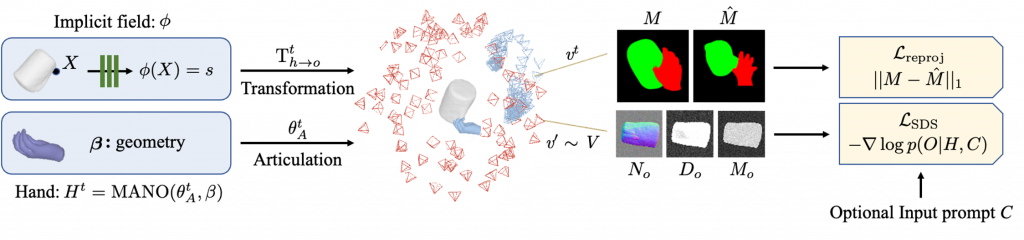
Method Figure: We compose the scene at time step t such that it can be reprojected back to the image space M from the camera pose vt. With an arbitrary view point v′, we then render amodal geometry cues for the object (surface normal No, depth Do, and mask Mo) as well as the hand. We expect the hand rendering H and an optional text condition on the object category, C, to be predictive of the object rendering O.
We first represent the HOI scene as hand and the object seperately. We have a time persistent Implicit field for the Rigid Object that can handle unknown object topologies. DeepSDF MLP layers are used to predict the Signed Distance Function (SDF to the object surface
ϕ(X) = s.
Parallely, we also have time varying Hand meshes at every time step t of the video. Given the texture of the hand (β) and its articulation (θtA) which are 10-dimensional and 45-dimensional respectively, we use a predefined parametric mesh model (MANO) to represent the hand dynamics.
Ht = MANO(β, θtA)
Given the time-persistent object representation ϕ and a time-varying hand mesh Ht, we then compose them into a scene at time t such that they can be reprojected back to the image space from the cameras. Since we don’t have access to the object templates, we track object pose with respect to hand Tth→o and initialize them to identity for the first frame. The rigid object frame can be related to the predicted camera frame by composing the two transformations: Ttc→h and Tth→o.
To differentiably render the HOI scene, we seperately render the object using volumentric rendering and the hand using mesh rendering to obtain 3 geometric cues: Normal, Depth and Mask, i.e Go ≡ (Mo,Do,No), Gh ≡ (Mh,Dh,Nh). To compose them into semantic masks, we then blend these renderings into HOI images by their predicted rendered depth:
M = B(Mh,Mo,Dh,Do)
Loss functions:
1. Hoi representation needs to be optimized to explain the input sequence. We therefore render semantic mask from estimated cameras (every frame) and compare the reprojection error from the the estimated original views with ground truth masks:
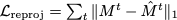
2. We need to optimize the scene to appear more likely from a novel view point. Scored distillation sampling treats the output of diffusion model as a critic to approximate towards more likely images (without backpropogating for efficiency). We therefore apply a loss on the reconstructed denoised signal Gio from the pretrained diffusion model:
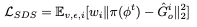
where v is a novel camera view, ϵ is the noise, and i is the time step.
Data Driven Prior for HOI Geometry:
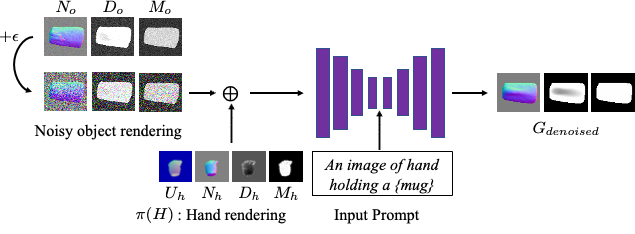
Figure: Geometry-informed Diffusion: Our diffusion model aims to take in a noisy geometry rendering of the object, the geometry rendering of the hand, and a text prompt, to output the denoised geometry rendering of objects.
We want to condition the diffusion model on category cues of an object (such as “cylindrical mug”) and hand cues (such as pinched hands imply thin handles). The diffusion model learns a data-driven distribution over geometry rendering of objects given its category C and the interacting hand H since it’s pretrained with large-scale ground truth HOIs. We use this learned prior to guiding per-sequence optimization and we expect the diffusion model to capture the likelihood of a common object geometry given C, H: p(ϕt|H,C). The diffusion prior basically helps to ensure that the novel views of the object are reasonable.
