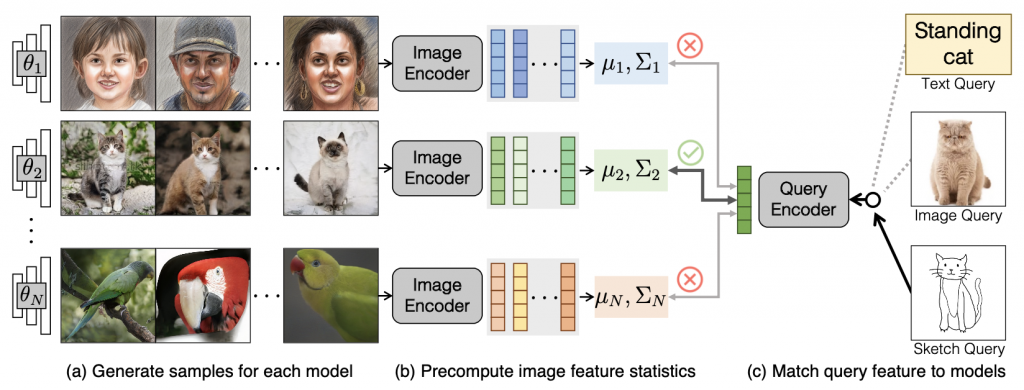
Method Overview. Our search system consists of a pre-caching stage (a, b) and an inference stage (c). Given a collection of models 𝜃 ∼ unif{𝜃1, 𝜃2, . . . , 𝜃𝑁 }, (a) we first generate 50K samples for each model 𝜃𝑛. (b) We then encode the images into image features and compute the 1st and 2nd order feature statistics for each model. The statistics are cached in our system for efficiency. (c) At inference time, we support queries of different modalities (text, image, or sketch). We encode the query into a feature vector and assess the similarity between the query feature and each model’s statistics. The models with the best similarity measures are retrieved.
Model retrieval is a challenging task: even the simplified question of whether a specific image can be produced by a single model can be computationally difficult. Unfortunately, many deep generative models do not offer an efficient or exact way to estimate density, nor do they natively support assessing cross-modal similarity (e.g., text and image). A naive Monte Carlo approach can compare the input query to thousands or even millions of samples from each generative model, and identify the model whose samples most often match the input query. However, such an approach can make model search too slow.
We first present a general probabilistic formulation of the model search problem and present a Monte Carlo baseline. To reduce the search time and storage, we “compress” the model’s distribution into precomputed 1st and 2nd order moments of the deep feature embeddings of the original samples. We then derive closed-form solutions for model retrieval given an input image, text, sketch, or model query. Our final formula can be evaluated in real-time.
Probabilistic Retrieval for Generative Models
Our goal is to quantify the likelihood of each model θn given the user query q, by evaluating the conditional probability p(θ|q). The model with the highest conditional probability is retrieved:
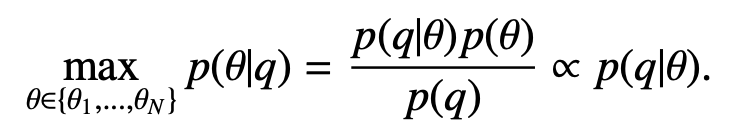
Since we assume the model collection is uniformly distributed, by Bayes’ rule it suffices to find the likelihood of the query q given each model θ instead. There are two scenarios to infer the conditional probability p(q|θ):
(1) When q shares the same modality with θ (e.g., searching image generative models with image queries), we directly reduce the problem to estimating the generative model’s density.
(2) When q has a different modality to θ (e.g., searching image generative models with text queries), we take account of cross-modal similarity to estimate p(q|θ). We discuss the two cases in the following.
Image-based Model Retrieval
Given an image query q, we directly estimate the likelihood of the query p(q|θ) from each model. In other words, the best-matched model is the one most likely to generate the query image. Since density is intractable or inaccurate for many generative models, we approximate each model by a Gaussian distribution of image features. We sample images from each model, denoted by x. We obtain the image features z = ψim(x), where ψim is the feature extractor. Now we express p(q|θ) in terms of image features z.
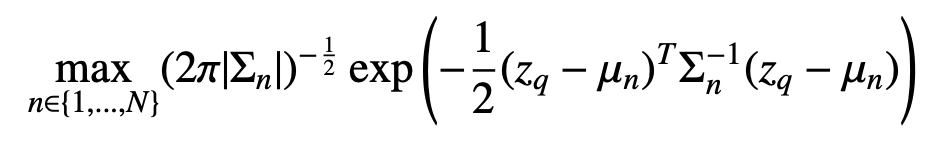
where the query image feature is denoted by zq = ψim(q), and each model θ is approximated by p(z|θ) ∼ N(µn, Σn). We refer to this method as Gaussian Density.
We can use the same method for sketch-based model retrieval if the embedding network ψim also works for human sketches. In our experiment, we find that CLIP can produce similar feature embeddings for similar images and sketches. CLIP outperforms other pre-trained networks (e.g., DINO) by a large margin.
Text-based Model Retrieval
Given a text query q and a generative model p(x|θ) capturing a distribution of images x, we want to estimate the conditional probability p(q|θ).
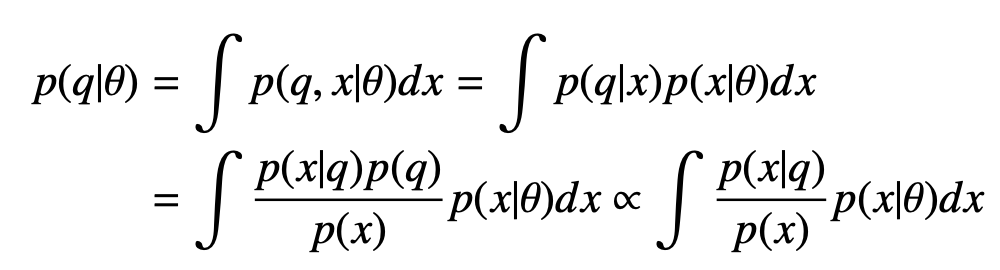
Here we assume conditional independence between query q and model θ given image x, so p(q|x, θ) = p(q|x). We apply Bayes’ rule to get the final expression. The text query q may correspond to multiple possible image matches p(x|q), and we estimate the term p(x|q)/p(x) using cross-modal similarities. In fact, this expression is proportional to the score function f in contrastive learning (e.g., InfoNCE), where f(x, q) is proportional to p(x|q)/p(x). Since CLIP is trained on a text-image retrieval task with the InfoNCE loss, we can directly apply the pre-trained CLIP model to simplify the above equation.
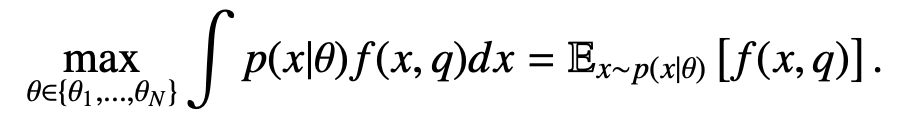
We recall that CLIP consists of an image encoder φim and a text encoder φtxt, and it is trained with a score function based on cosine similarity:
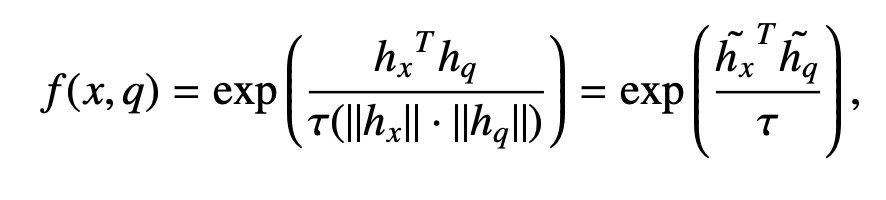
where hx = φim(x) and hq = φtxt(q) are the image and text features from CLIP, respectively. h˜x = hx/||hx|| and h˜q = hq||hq|| are the normalized features. Hence, Equation 5 can be written precisely as:
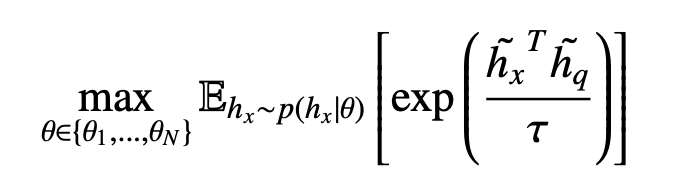
Now we have a tractable Monte Carlo estimate of the integral. We sample images from each model and average the score function of each image sample x and the text query q. We refer to this method as Monte Carlo. However, directly applying Monte Carlo estimation is inefficient in practice, since we need lots of samples to yield a robust estimate. To speed up computation, we provide two ways to approximate the above equation. First, we find that a point estimate at the first moment of p(hx|θ) works well. We directly estimate the cosine distance between the mean image features and the query feature. Since the exponential and temperature mapping is monotonically increasing, the matching function becomes:
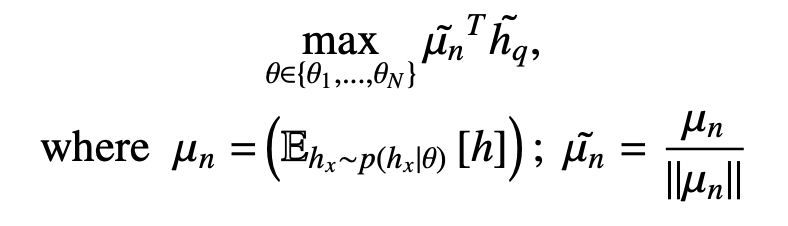
We refer to this method as 1st Moment. We can also approximate p(hx|θ) using both the first and the second moment to get the following expression.
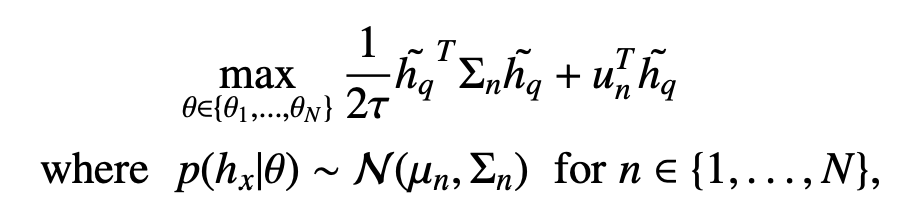
We refer to this method as 1st + 2nd Moment. Empirically, the performance is similar between approximation to the first or second moment. We provide more analysis in the paper.
Extensions
Multi-modal query. We can further extend our model search to handle multiple queries from different modalities. To achieve this, we use a Product-of-Experts formulation [Hinton 2002; Huang et al. 2021] wherein the final likelihood of a model, given a multimodal query (e.g., text-image pair), is modeled as a product of likelihoods given individual queries followed by a renormalization.
Finding similar models. Once a model is found, we enable navigation to similar models. To compute the similarity between models, we use the Fréchet Distance [Dowson and Landau 1982] between the models’ feature distributions. Following prior work [Heusel et al. 2017a; Kynkäänniemi et al. 2022], we approximate a model’s distribution by fitting a multivariate Gaussian in an image feature space. Then the Fréchet Distance can be computed directly from the Gaussian parameters. For each model, we pre-compute a list of similar models based on the smallest pairwise distances.
User Interface

The user interface of model search. The user can enter a text query
and/or upload an image in the search bar to retrieve generative models
that best match the query. Here we show the top retrievals for the text query
“animated faces,” which shows StyleGAN-NADA models [Gal et al. 2022]
trained on animated characters.
We create a web-based UI for our search algorithm. The UI supports searching and sampling from deep generative models in real time. The user can enter a text prompt, upload an image/sketch, or provide both text and an image/sketch. The interface displays the models that match most closely with the query. Clicking a model takes the user to a new page where they can sample new images from the model. The website employs a backend GPU server to enable real-time model search and image synthesis capabilities.
References