Our methodology involves the use of the Structure-from-Motion (SfM) and other external optimization strategies from Colmap to estimate the camera intrinsics.
We input camera extrinsic and images captured from various viewpoints and obtain improved camera intrinsics parameters as output. Merely relying on the Structure-from-Motion approach does not yield sufficiently accurate camera intrinsic values. Hence, we incorporate Kruppa equations for self-calibration to acquire an initial camera intrinsics estimate, which we then utilize as an input to our pipeline.
Structure-from-Motion Pipeline:
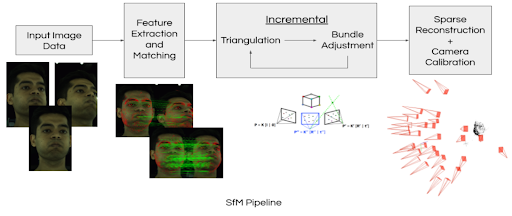
The SfM pipeline proceeds as follows:
- Image features are extracted from every image and matched to identify the overlapping part of the scene between every image pair
- 3D world coordinates and camera poses are obtained through the triangulation of matched points in each image pair. New points and matches are incrementally added with each additional image.
- Bundle adjustment refines 3D point coordinates and camera poses by minimizing the reprojection error. The accuracy of the 3D model is progressively improved as more images are added and the bundle adjustment is iteratively applied.
Kruppa equations
Kruppa’s equations, which are widely known as the first camera self-calibration method were first developed and used in the early 2000s. However, these equations are extremely sensitive to noise.
Given,
- F – Fundamental Matrix between any camera pair
- A, A’ – Unknown intrinsics of the camera pair
- K = AA^T
We use the relationship between the essential matrix and fundamental matrix to eliminate all the unknowns and establish a relationship between the Fs and Ks of the camera pairs. This gives us 6 equations per camera pair out of which only 2 of them are linearly independent. Hence, for m cameras, we will have m*(m-1) equations to solve for 4*m unknowns (camera intrinsics – fx, fy, cx, cy).
Classical Kruppa Equations –
Advanced Feature Detection and Matching
SIFT Features: A critical step in a typical SfM pipeline is to first compute a set of visual features in each image, such as SIFT features, and correlate them between the images. However, triangulation and bundle adjustment are sensitive to the accuracy of these features. If they are positioned incorrectly, the results of the optimization will contain some error and might not converge. Typically, a threshold is set on the quality of the SIFT feature correspondences to reduce the likelihood of outliers throwing off the results.
Better Features and Matches:
Our goal is to improve the results of this optimization by introducing other high-quality point correspondences into the objective to supplant the rejected low-quality features.
Alternative Methods: We incorporated several techniques into the feature selection step:
- Replacing SIFT features with deep learning-based detector and descriptor frameworks or face keypoint detection
- We use SuperPoint frameworks to detect key points because it can repeatedly detect a much richer set of interest points than traditional corner detectors. We expect that it helps the SfM pipeline to average out the keypoint localization noise and result in a more accurate triangulation. To match the key points we use the SuperGlue model, an attention-based graph neural network. We believe that SuperGlue provides with higher number of accurate matches due to its self-attention and cross-attention mechanisms.
- We also perform keypoint detection for facial features, such as the corners of the mouth and the tip of the nose, on faces present in the scene. This adds additional, high-quality correspondences that the SfM solver can then optimize against.
- Filtering key points based on their proximity to significant parts of human faces.
- Featuremetric key point location adjustment to all of the detected key points before feeding them to the SfM pipeline.
- For all of the detected key points, we apply keypoint location adjustment by optimizing its feature-metric consistency across tracks.
SuperPoint Keypoint Descriptors and SuperGlue Keypoint Matching
- We extract key points using the self-supervised interest point detector SuperPoint and match them between each pair of images using the attention-based neural network, SuperGlue.
- To ensure a comparable evaluation with 15,000 SIFT key points, we extracted the same number of SuperPoint key points per frame and applied a 0.9 score threshold to filter SuperGlue key point correspondences and establish meaningful matches.
- We expect SuperPoint key points to help the pipeline by increasing the key point’s repeatability and rejecting some spurious detections. Moreover, a bigger set of interest points provided by SuperPoint facilitates the pipeline to average out the geometric noise. We also assume that the SuperGlue model provides us with better keypoint matching due to the attention-based mechanism encoding contextual information about the scene and analyzing both keypoint appearance and position.
- Due to resource limitations, we used pre-trained SuperPoint and SuperGlue networks.
Facial Keypoint Detection
- For each frame, we perform inference using a pre-trained facial feature keypoint detector.
- This outputs a set of 217 labelled key points corresponding to predetermined locations on a face, such as the corners of the mouth, the tip of the nose, etc.
- We hash the keypoint ID j into a 128-bit descriptor to align with COLMAP’s expectations for feature descriptor shape.
- Moreover, facial key points provide meaningful matches even between images with small scene overlaps. We expect to obtain more useful matches, and consequently, better camera calibration using the facial keypoint detections.

