Overview

Our previous approach to depth estimation contains three main submodules: unary feature extraction, 3D spherical sweeping, and cost volume computation. We have done experiments to optimize the 3D volume computation network and choose different CNN models to extract the unary features, such as deformable, or spherical convolutions, but the improvements were very minimal. Thus we transitioned to use the recent foundation model with transformer-based architecture, DINOv2 [1], which enables us to leverage pre-trained models to achieve greater efficiency and potentially improved performance.

About DINO

DINOv2 employs self-supervised learning to train a Vision Transformer on a curated dataset of images. This process produces versatile visual features that can be applied across different image tasks without fine-tuning.

DINO – Depth Estimation decoder

For depth estimation, DINOv2 employs a DPT decoder head, which allows for detailed and dense depth predictions. Specifically, the DPT [5] first reassembles tokens from multiple transformer stages into image-like representations, at different scales, and applies fusion modules to merge these representations progressively to predict depth. DINOv2  also provides simpler linear decoders, but the DPT head is our primary focus due to its better performance.

DINO – Depth Estimation Results

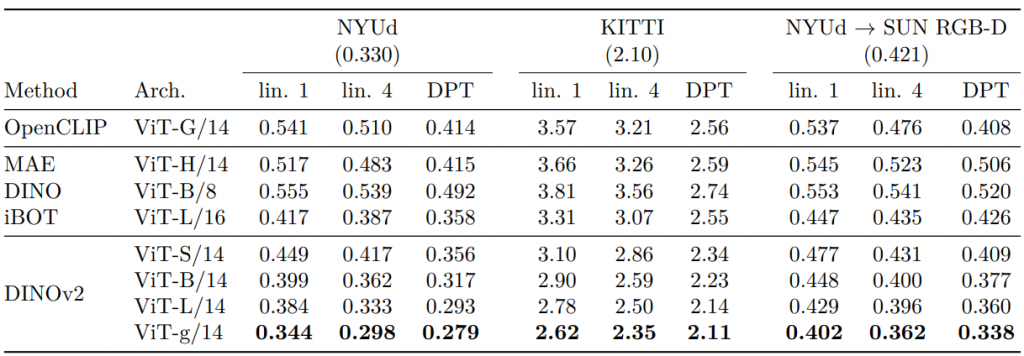
Here’s a result table for depth estimation. These methods are measured using the RMSE metric across three datasets, with lower indicating better performance. DINOv2 with the DPT head performs better against the listed state-of-the-art self-supervised learning models. 

DINO with fisheye

But the question remains – how does DINOv2 perform with distorted images? As shown in the example below, the DINOv2 could give a coarse depth prediction, but it missed depth information across finer structures and curved surfaces such as the edge of the bench. Thus we also need to investigate ways to make DINOv2 more distortion invariant.

DarSwin – Polar Patch Partition

Recent research like DarSwin [2] offers insights into adapting transformers for distorted images. Unlike standard patch embedding, DarSwin employs a distortion-aware Polar Patch Partition that respects the fisheye image’s unique features. It splits the image in the azimuth direction in an equiangular fashion, while the radial split follows the lens distortion curve, accommodating the inherent distortion of fisheye lenses.

DarSwin – Distortion-aware Sampling

Furthermore, DarSwin collects the same number of points within each patch and then feeds into the patch embedding layers. The result is the Darswin model can not only understand but also respect the fisheye distortion, leading to more accurate depth estimation. We leverage the same annular patching method to process the raw fisheye image directly instead of relying on square patches as in DINOv2.

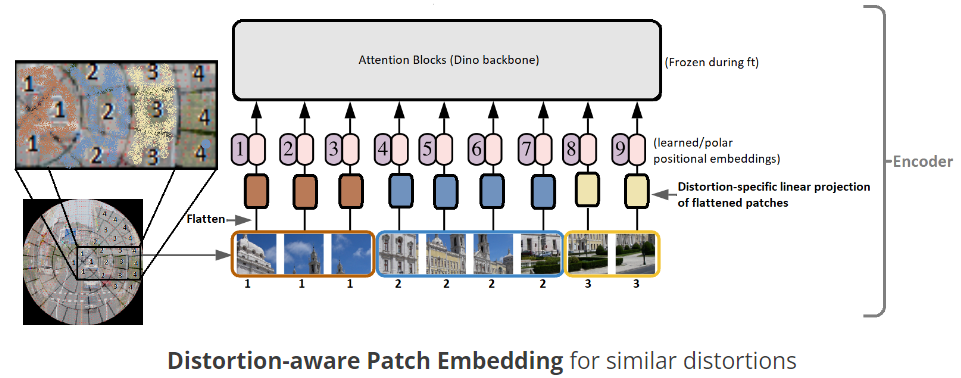
Distortion-aware Patch Embeddings

Once we apply the annular sector-based patching method to the input fisheye, we propose to use different linear projections for each set of distortion levels. The original ViT (and DINO) uses a single linear projection of all the square patches to get the individual visual tokens. But, given that the level of distortion changes radially in a fisheye image (increase from 1 to 4 in the below example), we apply a different learned linear projection for each of the distortion levels. The idea is that these learned projections also learn how to deal with the image distortion in those levels. Once we get these distortion-aware patches, we then add polar positional embeddings which are then fed to the attention mechanism like before.

Since the pixel distribution changes radially in fisheye images, we leverage polar embeddings from the SPE module [3] that rely on the sampled polar point (r, theta) instead of the traditional cosine or RelPos embeddings.

The polar positional embeddings can be expressed as below where (r, theta) represents the position of each sampling point. The sine and cosine functions in the i-th dimension of the
position encoding is modulated by a frequency parameter, and the power parameter is used to adjust the expressivity of the position encoding.

Overall architecture

The overall architecture from the annular patching approach, to distortion-aware patch embedding, to the polar positional encodings to get the visual tokens in the encoder are shown below. This is then fed to the DPT decoder to get the corresponding depth map in the fisheye space.

Results

We first compare the performance of the DINO approach against our baseline NDDepth [4] on pinhole images and then evaluate its performance on fisheye images directly. Below, we present some representative results in an indoor environment (house) with the 6 images collected from AirSim (Back, Bottom, Front, Left, Right, Top) and the respective depth estimation results from DINO and NDDepth. It can be observed that DINO results better capture fine-grained features from the input pinhole image than the baseline.

Next, we evaluate the performance of the DINO approach on a set of environments collected in AirSim and present their relative ground truth depths. From the metrics, it can be observed DINO does suffer from a higher error in fisheye space compared to the relatively easier pinhole space depth estimation.

The house environment is an indoor environment, and Gascola models an outdoor in-the-wild space while Victorian street models a more urban outdoor landscape. These three were selected and reported to test the performance on a range of environment settings.

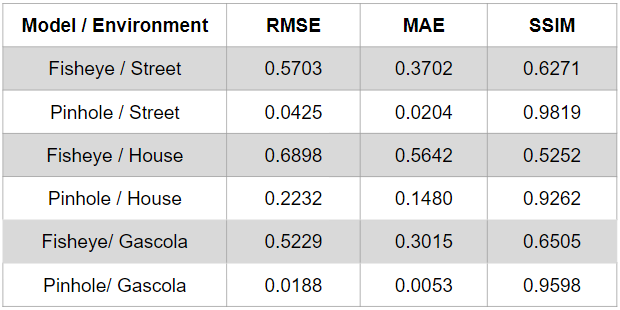
Note: The reported depth values were cut by range (0.001, 1.0)

References

[1] Oquab, M., et al. (2023). DINOv2: Learning Robust Visual Features without Supervision.

[2] Athwale, A., et al. (2023). DarSwin : Distortion Aware Radial Swin Transformer. IEEE/CVF International Conference on Computer Vision (ICCV).

[3] Yang, D., et al. (2023). Sector Patch Embedding: An Embedding Module Conforming to The Distortion Pattern of Fisheye Image.

[4] Shao, S., et al. (2023). NDDepth: Normal-Distance Assisted Monocular Depth Estimation and Completion. IEEE/CVF International Conference on Computer Vision (ICCV).

[5] Ranftl, R., et al. (2021). Vision Transformers for Dense Prediction. IEEE/CVF International Conference on Computer Vision (ICCV).