Introduction - Neural Synthetic Wavelength Interferometry

This project is an application of neural techniques to synthetic-wave interferometry. It aims to improve on the methods of Swept-Angle Synthetic Wave Interferometry (Kotwal et al. 2022) by replacing the current depth recovery pipeline with one that is capable of adapting to correlated sources of noise and measurement imperfections by learning a more robust phase recovery function than the one derived purely from theory.

Basics of Interferometry

At its core, synthetic-wave interferometry (SWI) is based on much of the same methods and principles as phase-shifting interferometry (PSI). The goal is to infer depth at each point of a scene by counting the (fractional) number of wavelengths that pass as a beam of light with known frequency departs a source, reflects off the scene, and is received by a sensor

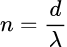
where d is the total distance travelled, λ is the wavelength of the beam, and n is the number of wavelengths that pass. This can be expressed as a phase

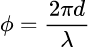
which is easier to measure since the phase is directly related (by a sine function) to the amplitude of the wave and thus the intensity image that is captured by a sensor.

In PSI and SWI, we are interested in measuring the correlation between the phase change of the source–scene–sensor path and the phase change of a known source–mirror–sensor path, in which a beam reflects off a mirror at a controlled position instead of off the scene. Since the latter path’s length is known, we can calculate the phase change of the former from the interference pattern that arises from light travelling along each of the two paths.

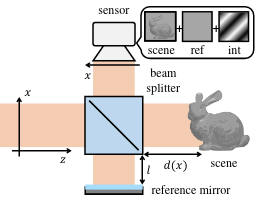
Figure 1. In both PSI and SWI, incoming light (from the left) is split into two paths, one to the scene and the other of known length. The resulting image contains interference which is used to recover the unknown phase differences at the scene. (From Kotwal et al. 2022.)

With the resulting image captured at four different positions of the reference mirror, we can use a well-known technique called the N-shift phase retrieval algorithm (with N = 4) to recover this phase difference.

Synthetic Waves

One drawback of the phase retrieval algorithm is that since it recovers phases from squared amplitudes (in the form of the captured image), it is only unambiguous up to one wavelength of the light used due to the periodic nature of sine waves. (This phenomenon is known as phase wrapping.) SWI extends this effective range by first interfering two light waves of similar frequencies, which results in an synthetic wave (also known as the envelope) modulating a carrier wave. The unambiguous range is now one wavelength of the envelope, which is much larger than one wavelength of the original waves used to form it.

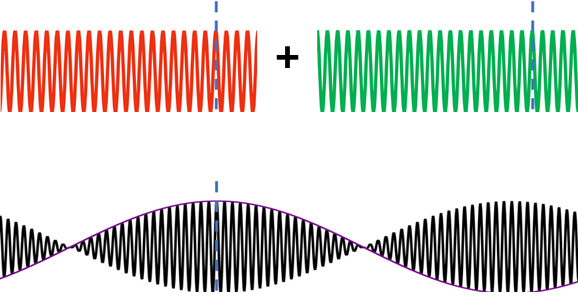
Figure 2. The light used to illuminate the scene in SWI is itself the sum of two waves of slightly-separated frequencies.

To account for the new high-frequency carrier signal embedded in the envelope, the four reference mirror positions are now each subdivided into four even more granular positions corresponding to four different phases within the carrier wave, for a total of sixteen images captured per scene. A modified version of the N-shift phase retrieval algorithm, known as the M,N-shift phase retrieval algorithm (with M = N = 4), is used to recover the phase difference between the scene and reference signals on the synthetic wavelength.

Figure 3. Images are captured at sixteen positions of the reference mirror corresponding to sixteen positions along the synthetic wave.

Proposed Method

This classical phase-retrieval pipeline contains at its core a maximum-likelihood estimator of the phase differences in the scene. It is informed by a physics model of the capture setup and assumes a Gaussian noise distribution where errors in any given pixel and frame is uncorrelated with those in other pixels or frames. What this means is that the output of the pipeline may not be the most accurate output that could be recovered from the information contained within the frames. In particular, there are several reasons to believe that we can do better:

It is likely that noise is correlated between pixels, for example if it arises from areal imperfections in the capture setup.
We have at our disposal a high-quality RGB image of the scene, which could provide a wealth of information about the scene’s noise distribution or phase properties.
Related work in ToF imaging (Baek et al. 2022, Su et al. 2018) have demonstrated improvements over other classical pipelines using neural nets, indicating that more information is available than the classical techniques capture.

Comparing the results of our classical pipeline to that of the slower but more robust optical coherence tomography (OCT), we do see room for improvement. In our experiments, the depth map generated by OCT is treated as ground truth.