Motivation
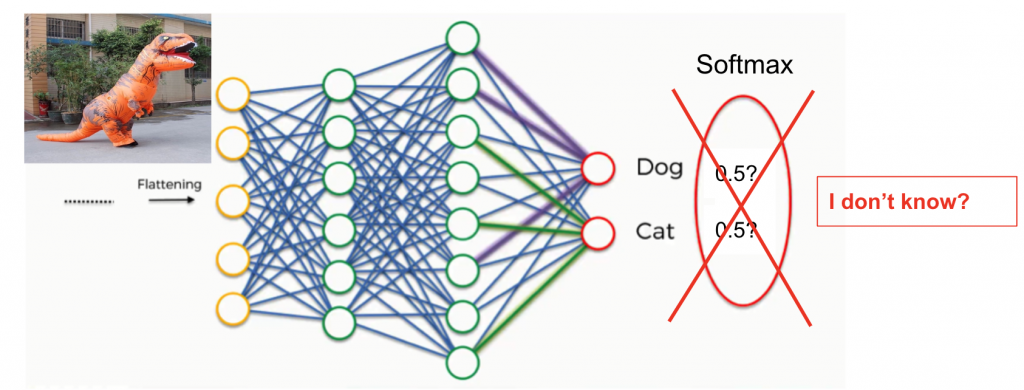
The accurate reflection of model prediction confidence is critical in the trustworthy usage of model artificial intelligence, especially in deep learning systems, often essentially considered black boxes. Thus the evaluation of prediction uncertainty is meant to let the system indicate “I am not sure” when the input data is ambiguous or out of distribution that the model fails to give a confident prediction. Often, model prediction is over-confidence, even on the mistaken class, which prevents machine learning from being applied to more error-sensitive areas like space technology.
Uncertainty Quantification
Uncertainty quantification is used to measure the difference between model-predicted confidence and actual performance. It’s a way of measuring if the network knows what it knows
In general, there are two kinds of uncertainty:
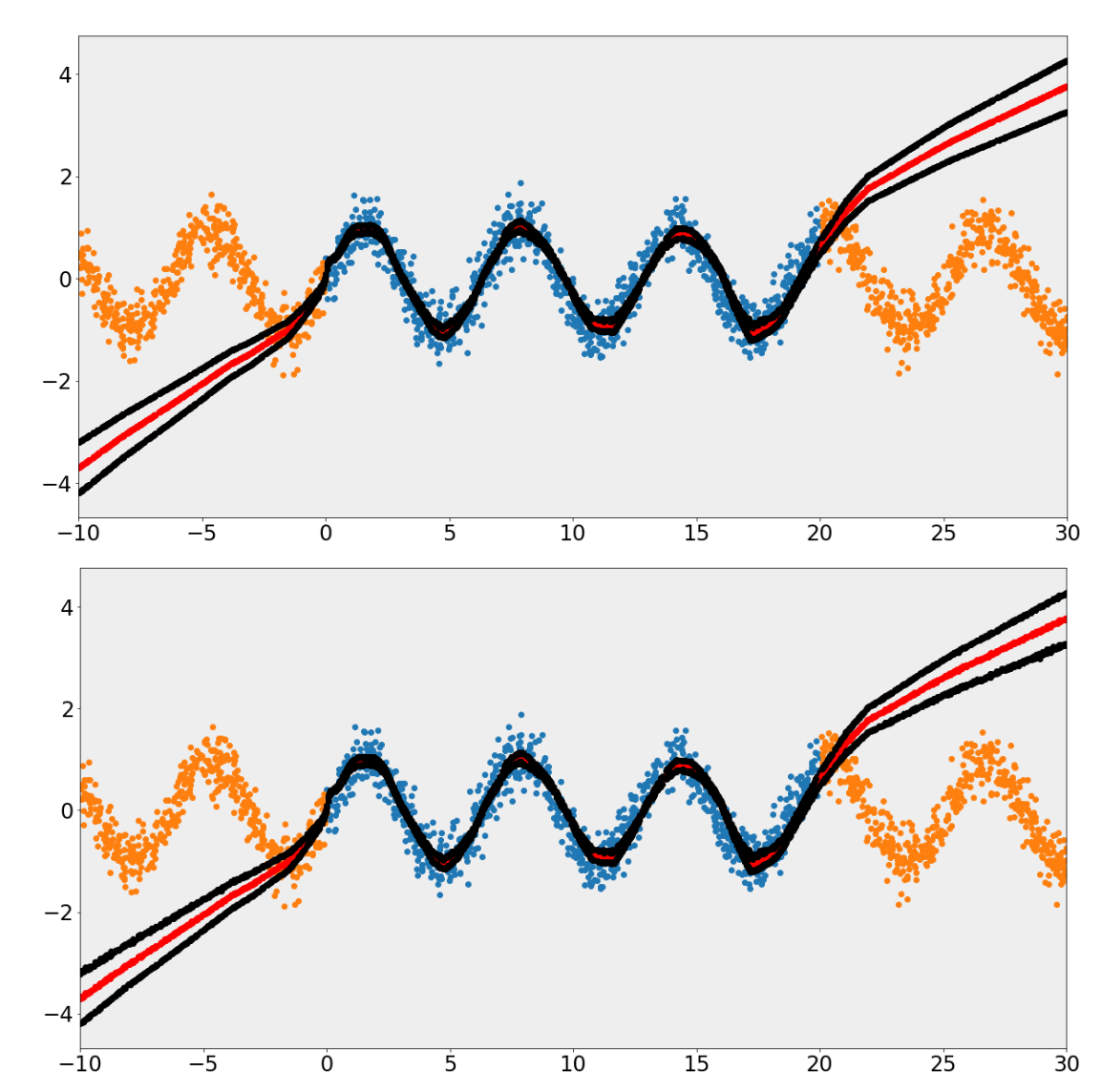
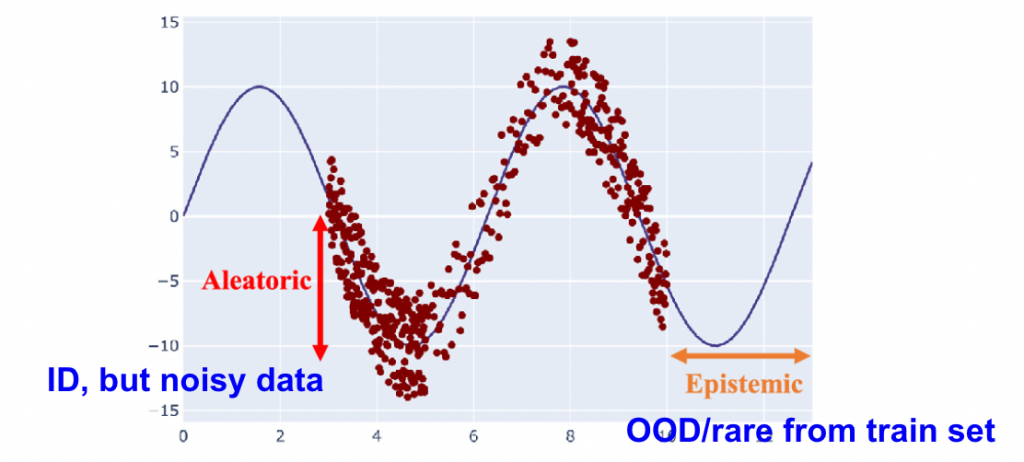
- Epistemic uncertainty (model uncertainty) due to lack of knowledge( for instance, Out of-distribution (OOD) data). Often reducible by adding more data. It’s sensor agnostic. It’s a modeling of how same models from different weight initialization vary in prediction when they were trained on the same dataset.
- Aleatoric uncertainty ( data uncertainty) due to noise in data. Often not reducible by adding more data and is only meaningful in distribution. It’s not sensor agnostic by definition.
Problem statement
Previous methods most fail between the trade-off of computation efficiency and usefulness. Most approaches currently rely on Monte-Carlo or other sampling methods to provide a distribution of predictions from which uncertainty can be calculated. This poses a real issue on run-time constrained scenarios such as self-driving where at worse, sampling increases runtime linearly with number of samples. For instance, model ensemble[1] and Mote-Carlo Dropout[2] is still the SOTA in this field. In this project, we propose to investigate ways to estimate both epistemic and aleatoric uncertainty in real-time detection with a deterministic single pass method.

Reference:
[1] Gal, Yarin, and Zoubin Ghahramani. “Dropout as a bayesian approximation: Representing model uncertainty in deep learning.” international conference on machine learning. PMLR, 2016.
[2] Lakshminarayanan, Balaji, Alexander Pritzel, and Charles Blundell. “Simple and scalable predictive uncertainty estimation using deep ensembles.” Advances in neural information processing systems 30 (2017).