Photo-realistic human face rendering and reconstruction in essential to real-time telepresence technology that drives modern Virtual Reality applications. Since humans are social animals that have evolved to express and read emotions from subtle changes in facial expressions, tiny artifacts give rise to uncanny valley that could hurt the user experience. Nowadays, many modern 3D telepresence methods leverage deep learning models and neural rendering for high-fidelity reconstruction, and to tackle difficult problems such as novel view synthesis and view-dependent effects modeling. These approaches are usually data-hungry, and the design of a capture system and data collection pipeline would directly determine the performance of those models. To this end, we introduce a dataset created by Mugsy, a multi-view capturing system. We then use a conditional VAE model as our baseline and evaluate model’s reconstruction quality with respect to different network architectures, including spatial bias, texture warp field and residual blocks. Empirically, we find out that baseline model is beneficial from these network architectures on interpolating novel viewpoint while we do not observe the same improvement of model’s performance on generalizing to unseen expressions.
Our model greatly resembles the Deep Appearance Model~\cite{10.1145/3197517.3201401}, which is a VAE model that takes meshes and average texture as input and decodes the view-dependent textures for rendering. We regress the relative displacement for each vertex in the mesh on the normalized ground-truth data. The input texture is the average texture from each camera of a certain frame. The decoder is given the camera position from which the face is being viewed, and tries to predict the texture that renders to the ground-truth screen image from that camera view. We use Nvdiffrast\cite{nvdiffrast} for differentiable rendering to propagate gradients from screen images to the predicted textures. The input textures are normalized by an average texture across all expressions and views of the whole dataset, and the model also generates predictions in the normalized texture space. When calculating loss, a mask is provided by the renderer because we only care about the parts that can be covered by the face texture, where the gradients flow. The mask is obtained by rendering a facial texture mask to screen space. The facial texture weight mask is manually annotated that assigns different weights to different part of the face texture. This is because humans are more sensitive to certain regions such as eyes and mouth, and we want to make the model focus on these parts. Formally, the loss function is given by $L = \lambda_1 \left |M(v, \hat{T})\odot (R(v, \hat{T}) – I)\right |^2 + \lambda_2 \left | \hat{G} – G \right |^2 + \lambda_3 KL(N(\mu_z, \sigma_z) || N(0, I))$, where $M$ and $R$ denotes the screen masking and rendering functions respectively, $v\in \mathbb{R}^3$ is a camera view vector, $\hat{T}$ is the predicted texture by decoder, $I$ is the ground-truth screen image, $\hat{G}$ is the predicted geometry, $G$ is the ground-truth geometry, $\mu_z$ and $\sigma_z$ are the mean and variance of the latent distribution. For faster convergence and unequal learning rate, we multiply the output mean of encoder by $0.1$ and the log standard deviation by $0.01$. We use Adam\cite{adam} optimizer and perform 200K iterations for all the experiments. In practice, the masking function assigns higher weights to eyes and mouth regions since these parts are more important in human communication. This mask can be acquired by rendering a weight texture to the frame being trained on. We set $\lambda_1 = \lambda_2 = 1$ and $\lambda_3=0.01$.
\subsection{Model}
Our model follows a VAE design, where the encoder consists of 8 convolutional layers, each with kernel size 4 and stride 2, that downsamples the input texture from a resolution of 1024 to 2. For the mesh input, we simply encode it with a multi-layer perceptron (MLP). On the decoder side, the view information is fed into an MLP and the feature is concatenated to the latent code. Thus, the texture decoder can be conditioned on this view information and models view-dependent effects in texture. We explore several different architectures to investigate their generalizing capacity on novel expressions and camera views.
\paragraph{Color Correction}
Since different cameras could have different color space, we optimize color correction parameters for each camera. Color correction is performed on the output texture by scaling and adding a bias to each RGB channel. The scaling factors and biases are initialized to 1 and 0, respectively. We fix the color correction parameters of one camera as an anchor and train the other parameters as a part of the model. Applying color correction is necessary, otherwise the reconstruction error will be dominated by the color difference instead of exact colors of the pixels.
\paragraph{Spatial-Bias}
For convolutional layers in the decoder for upsampling, instead of adding the same bias value per channel in the feature map, we add a bias tensor that has the same shape as the feature, meaning that each spatial location has its own bias value. In this way, the model is able to capture more position-specific details in the texture, such as wrinkles and lips.
\paragraph{Warp Field}
We can also decode a warp field from the latent space and bilinearly sample the output texture with the warp field. Conceptually, texture generation can be decomposed into 2 steps: a synthesized texture on a deformation-free template followed by a deformation field that introduces shape variability. Denoting by $T(p)$, the value of the synthesized texture at coordinate $p = (x, y)$ and by $W(p)$, the estimated deformation field, we consider that the observed image, $I(p)$, can be reconstructed as follows: $I(p) = T(W(p))$, namely the image appearance at position $p$ is obtained by looking up the synthesized appearance at position $W(p)$. Technically, we obtain a warp field as Deformable Autoencoders\cite{dae} does by integrating both vertically and horizontally on the generated warping grid to avoid flipping of relative pixel positions.
\paragraph{Residual Connection}
We can insert residual layers\cite{resnet} into our network to make it deeper. We investigate whether this increase in model capacity would make it generalize better.
To examine model’s generalization ability, we have 3 sets of evaluation, which will tell us model’s interpolation capacity on either novel viewpoint, or novel expression, or on both novel viewpoint and expression:
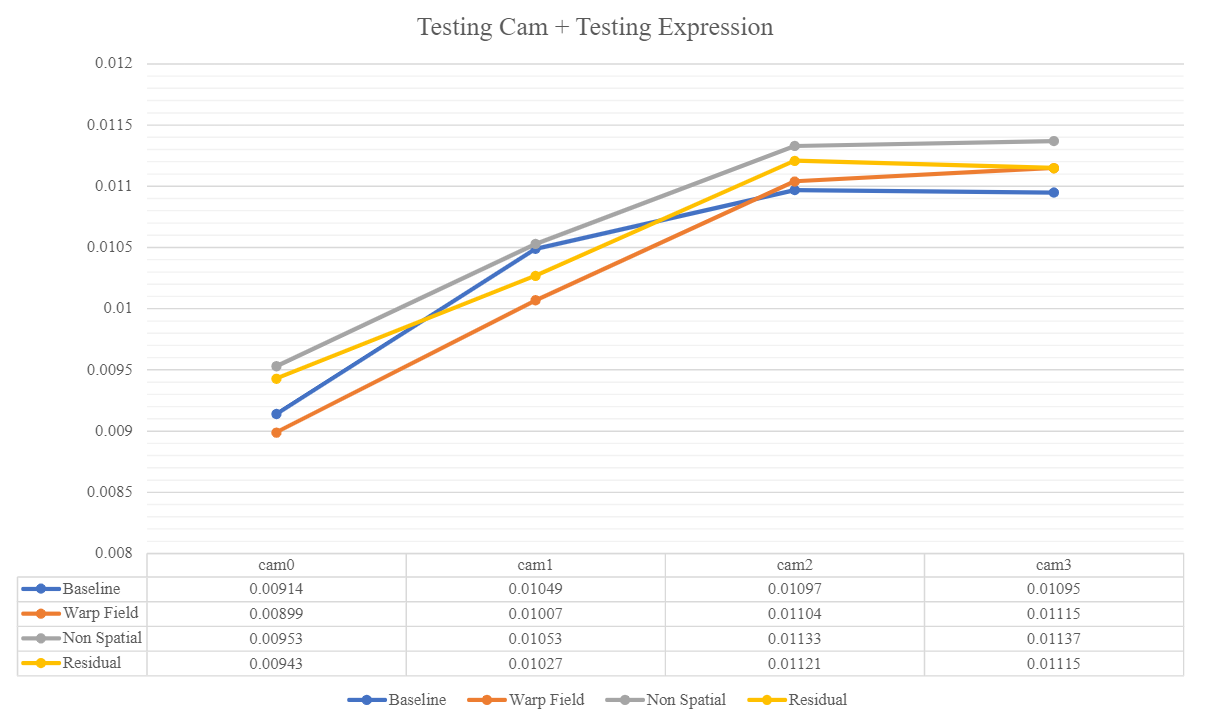
- Testing Camera on Testing Expression (Generalization on Viewpoint + Expression):
- Testing Camera on Training Expression (Generalization on Viewpoint):
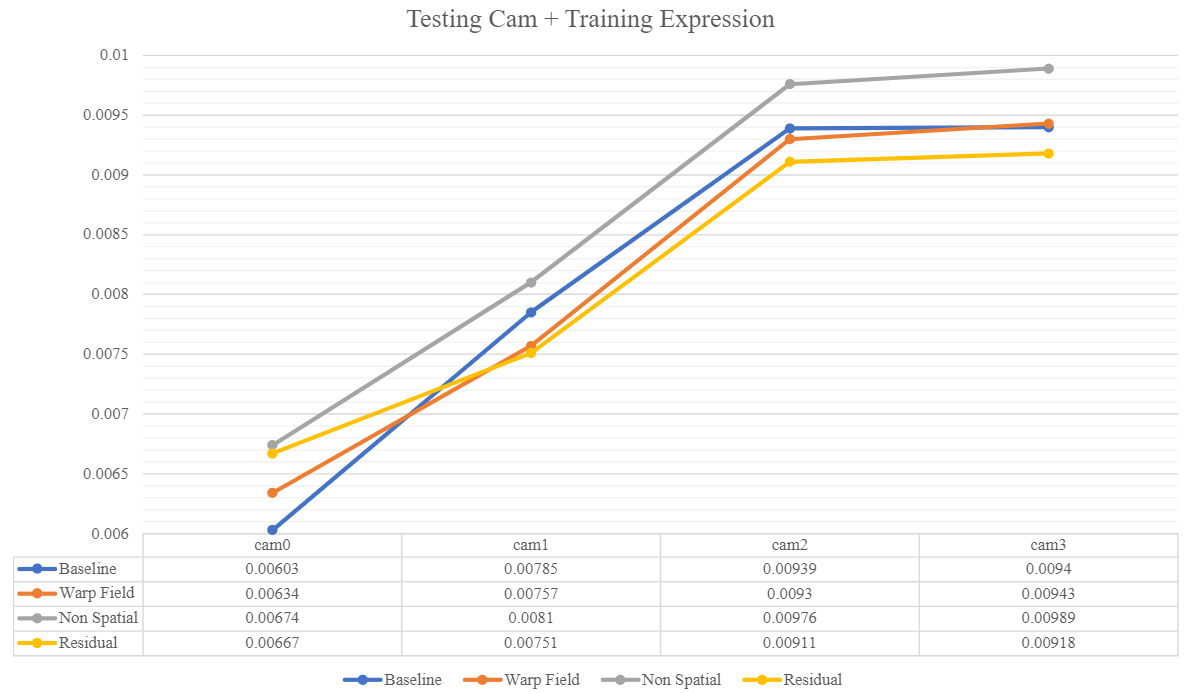
- Training Camera on Testing Expression (Generalization on Expression):