Left: Sample of our highly non-rigid point cloud
Right: Colored visualization of the learned dense per-point embeddings
Introudction
Representation learning is a core field in deep learning, especially in computer vision. Often times the final goal of many tasks, such as classification and segmentation, is to learn a good representation. And also, a good pre-trained representation could probably boost the model’s performance significantly. Recently, there is a rising interest in robot laundry folding tasks, as shown in Figure 1. But these tasks are very challenging because they involve objects that are highly non-rigid. To approach this problem, we propose to learn a representation for these kinds of deformable objects. And we decided to use point cloud to capture these objects because it can capture the rough 3D shapes without losing much detail. So our aim is to learn an embedding for every point in a point cloud. We imagine if we can successfully learn the dense embeddings of a point cloud, these pre-trained embeddings could significantly benefit some downstream tasks, such as training the reinforcement learning models to do laundry folding.

Overview
This project aims to learn a dense per-point embedding for highly non-rigid point clouds using self-supervised flow estimation. Two stages are involved in this project, namely flow estimation and embedding learning. We first construct a model to estimate flow between two point clouds in consecutive frames, and then adopt triplet loss based on the estimated flow to train another model that can generate per-point dense embeddings for any point cloud.
Dataset
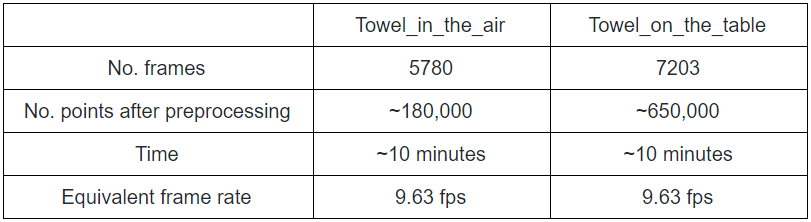
We collected two real-world datasets and three . They are all a sequence of point clouds deforming in arbitrary ways. The real-world datasets include two data sequences, namely towel_on_the_table and towel_in_the_air. They are both captured by 3 synchronized cameras into a single video sequence. Figure 2 shows one frame of data in 3 different camera viewpoints. Each image is associated with a depth map. So they are RGB-D images.

Viewpoint 1 
Viewpoint 2 
Viewpoint 3
Now we will introduce the steps we took in data preprocessing. Basically for each frame, we perform the following steps:
- Triangulate pixels in the 3 RGB-D images into point clouds using camera matrices
- Concatenate the 3 point clouds from 3 synced cameras into a single point cloud
- Box filtering: Apply a box filter tight around the towel to remove unrelated points
- Downsampling
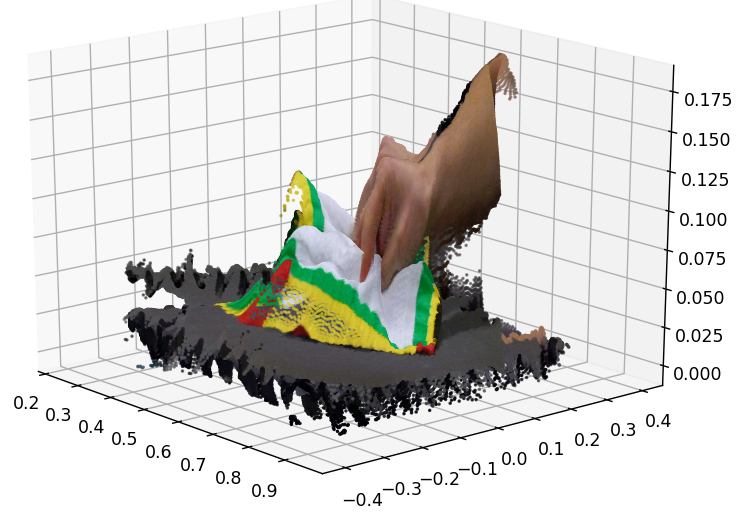
towel_on_the_table example 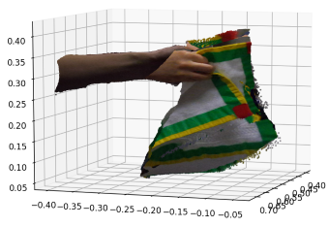
towel_in_the_air example
We show the statistics of the two real-world datasets in Figure 5.
Some examples of the collected synthetic datasets are shown in Figure 6. The datasets are collected using Blender and Softgym. Some data sequences capture random movement of the virtual grippers, while some capture folding and manipulating actions of the T-shirt.
Method
We observe that the movement of objects are usually captured by a sequence of video. What if we first learn a flow that captures the deformation of the object between two consecutive frames, and then use the flow to facilitate or even supervise the embedding learning task? Here is our proposed method. The first step is to train a flow estimation network that moves the point cloud in the first frame as close as possible to the point cloud in the second frame. And then, after we have the alignment between every point in the two point clouds, we can apply a triplet loss to learn the embeddings.
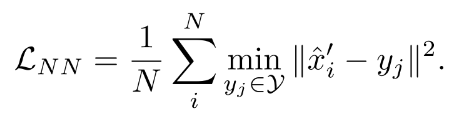
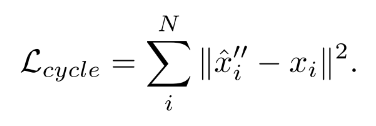
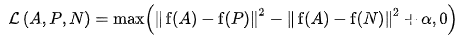
A: Anchor inputs
P: Positive inputs from the same class as A
N: Negative inputs from a different class from A
f: Embedding function (our network)
Alpha: A hyperparameter that represents the margin distance between positive and negative pairs
The formula of triplet loss is shown here. Minimizing this objective means we want to minimize the distance between embeddings from the same class, while maximizing the distance between embeddings from different classes.
In our case, we want to train an Autoencoder-like network that generates an embedding for every point in a point cloud. To apply triplet loss, we will feed two consecutive point clouds into the network and extract an embedding for every point. Then the point pairs aligned by the estimated flow will be a positive pair and should have similar embeddings. The point pairs not aligned by the estimated flow will be a negative pair and should have different embeddings.
Refer to Scene Flow Estimation and Embedding Prediction sections for more technical details and results.
Evaluation Metrics
Now we introduce the evaluation metrics we used in assessing the performance of the embedding prediction model.
Metric 1: Point match error
For every point in point cloud 1, we compute the L2 distance between the predicted point and the ground truth point in point cloud 2. Then we normalize the error by the largest possible distance between any two points in a point cloud over the whole dataset. Then we aggregate this error for all points in the point cloud to get a final score.
Metric 2: Fraction of false positives
For every point in point cloud 1, we compute the number of points that are closer to the ground truth in descriptor space than the prediction. We normalize this number by the total number of points in the point cloud. Then we aggregate this fraction for all points in the point cloud to get a final score.
Metric 3: Average L2 distance of false positives
We compute the false positives in the same way as in metric 2. We take the mean L2 distance of the false positives from the ground truth. Then we aggregate this distance for all points in the point cloud to get a final score.
Conclusion
- Current method is only able to learn limited semantic meanings in the point cloud. More sophisticated labeling, such as per-point semantic segmentation labels, may be needed to provide the model with more information.
- Learning on non-rigid objects using point cloud representation is not very straightforward as using image-based representation, because internal connectivity is ambiguous when using point cloud to represent highly non-rigid objects. Other representations like mesh may be preferred.
- The extent of deformation is an important factor to control during learning. Larger or smaller deformation between consecutive training pairs brings different learning results.




