Methodology - Consistent Multiview Color Correction

Problem formulation

First, let’s briefly review our problem formulation of this project. We aim to do color correction without confounding the camera, lighting, and view effects in the lightstage system. We capture a set of ColorChecker images in our system. Given those images, we estimate the color transform for each camera. Thereafter, we can apply the pre-estimated color correction model to arbitrary sensor images captured by the cameras. The results would be visually pleasing images as you would see on the right in the figure below.

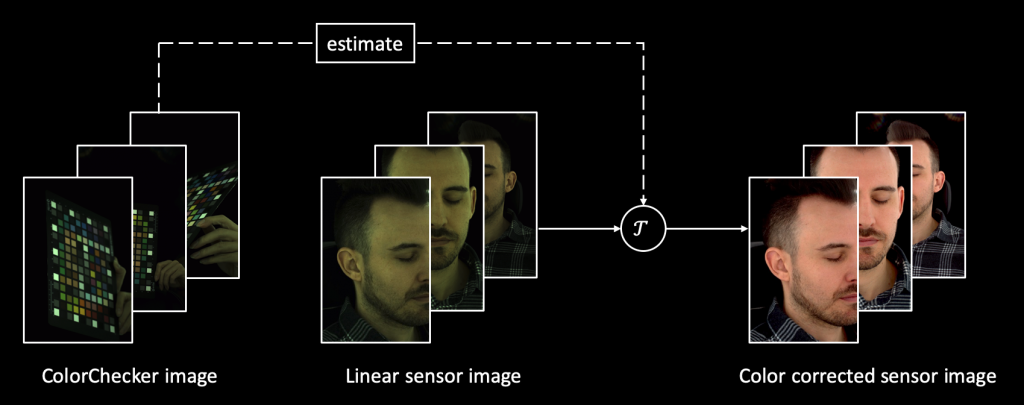
To solve this problem, we divide it into two parts: robust and efficient ColorChecker detection and consistent color correction, which we will introduce as follows.

ColorChecker Detection

To perform color correction for cameras, ColorChecker is widely used as an important tool by professional photographers. It contains a grid of colored patches, the reference colors of which are known under the standard D50 lighting. During the calibration process, users need to take an image of the ColorChecker and manually sample the colors from each individual patch. The color calibration can be performed in the sense that the dissimilarity between the sampled colors after correction and the reference colors are minimized.

Noticeably, One step mentioned above can be problematic in our more challenging problem setting. We have large quantities of images captured by different cameras at different time instants with a ColorChecker in them. It would be infeasible for us to exhaustively click on each color patch to sample those color values. Even worse, biased or imperfect color sampling will introduce noisy signals to the color correction step. This will severely affect the final quality of color correction. Therefore, it is necessary for us to develop a robust and accurate ColorChecker detection method.

At the first glance, this problem shouldn’t be too hard. We followed a common software Macduff as well as a related work to achieve this purpose. The idea is simple: we can use image processing methods to detect as many quadrilaterals as possible from the image; then we do the registration based on the color similarity.

*A common image processing based approach for ColorChecker detection*

But very soon, we find the existing approach doesn’t work well. We can observe many failure cases caused by different factors. Example failure results are shown below.

*The baseline approach can fail to obtain the number of patches in each row or column due to the inaccurate patch size estimation.*

*Another failure case. Seemingly locally fine predictions might fail in distant patches.*

Therefore, we aim to seek a more robust and fundamental solution to make our life easier. An intuitive solution is treating all the corner points of each color patch as keypoints of interest and we can adopt off-the-shelf keypoint detectors for human pose estimation to solve it. The major challenge lies in the lack of sufficient training data for our ColorChecker scenario. Fortunately, we find that training on synthetic datasets is sufficient to produce an extremely robust and accurate ColorChecker detector:

*Overview of the synthetic dataset generation. We augment the pose of the ColorChecker model in the 3D space and do the rendering over random natural background images.*

The tricks lie in various augmentations we develop to make the generated data as realistic as possible so the domain gap is negligible. Some example augmentations we perform are shown here.

*We multiple each channel of the texture with random tuplet of values uniformly sampled.*

*We can even capture real images of the ColorChecker to generate realistic textures based on corner point detection.*

Here is an illustrative video to show the robustness and generalization ability of our model in the single view setting. Furthermore, we can do geometric postprocessing to make our detection more robust: solve a PnP problem in the single view setting, or even do triangulation in the multiview setting.

ColorChecker Detection Demo (frame by frame prediction without tracking)

Color Correction

Since we have solved the ColorChecker detection problem in our multiview system, we can accurately sample color values from each individual patch of the ColorChecker. The remaining problem is how to estimate the color transform for all the cameras.

We can first look at a standard approach. We let someone hold the ColorChecker and stand in the system. We run our ColorChecker detector over the images of the captured ColorChecker. Then we can sample a set of color values from each individual patch. Since we are doing it in a linear color space. We use affine models to represent the color transform, and solve it in a least-squares sense: the distance between the affine transformed sampled values and the absolute reference values is minimized.

*A well-adopted approach for color correction*

It sounds reasonable and straightforward. We can look at some example results:

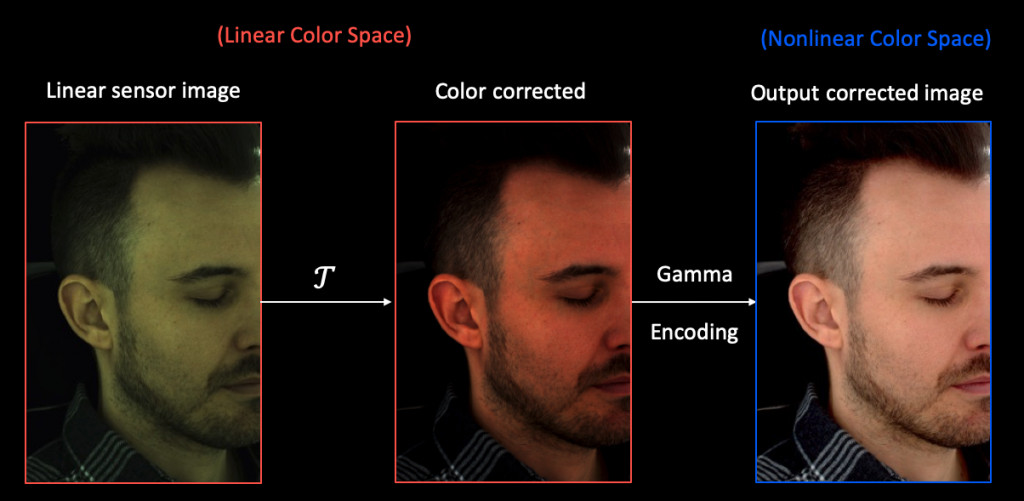
*We can see after color correction, the colors on the human face look more visually pleasing.*

But there’re some implicit assumptions hold in the formulation: we only considered the camera variability but ignored the lighting and view effects. These effects are entangled with the entire color correction process. Our life gets easier due to these simplifying assumptions, but what’s the cost? The answer is inconsistent color correction between cameras.

*After color correction by the standard approach, we observe inconsistency between different cameras.*

We need something fancier to tackle these limitations. Our idea is inspired by inverse rendering, which is the problem of estimating one or more of illumination, reflectance properties and shape from observed appearance (i.e. one or more images). The additional but vital ingredient specific to our problem is the sensor effect – the color correction model.

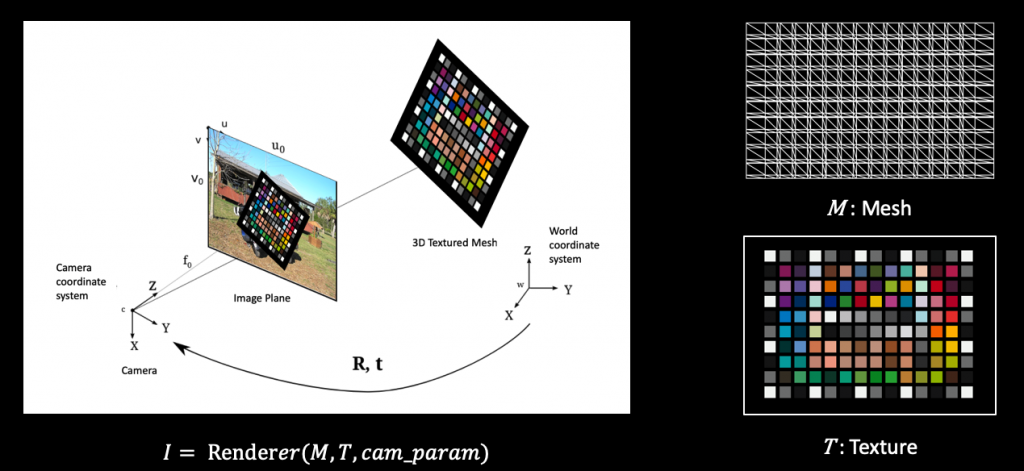
In a standard inverse rendering view, imagine that we have a renderer which takes in the albedo, normal vectors, and environment lighting as inputs, and produces a rendered image of the object. We can optimize the dissimilarity between the rendered image and our observation to recover the underlying variables (albedo, normal vector, and illumination) which explain our observation best.

Here our observation is a collection of ColorChecker images. We know its normal vector since we perform the detection in 3D space. We can also use the absolute reference color values under D50 lighting as the albedo. We produce a rendering, but we need to additionally apply a camera-specific correction model over it, which is still an affine transformation here. Then we can optimize it towards the observation we have. In this way, we are jointly estimating the color correction model and lighting parameters. We use the parametric illumination model proposed in this work.

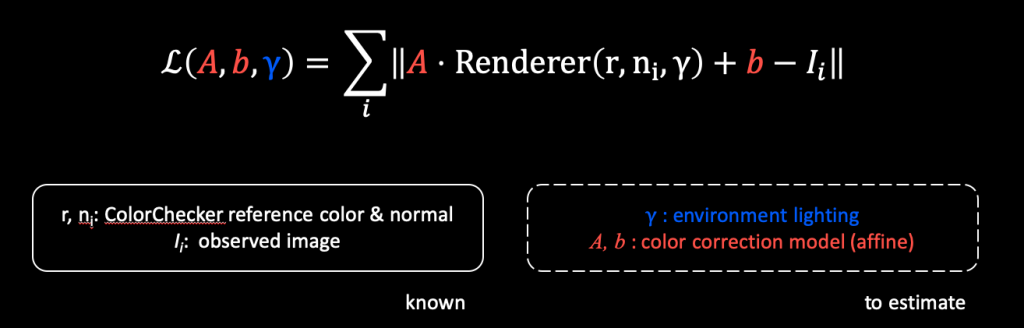
*The formulation of an inverse rendering perspective of color correction.*

This time we observe better consistency between color correction for different cameras.

*Example color correction results for different cameras by our inverse rendering based approach.*

Note the color looks dimmer in the figure above. It’s caused by the scale ambiguity between the affine transformation and the lighting model in our loss formulation. This issue can be addressed by a white-balancing process.

Please do check our presentation videos if you are interested in more details and more fancy results 🙂