In this section, we delve into the methods employed for surface reconstruction. We experimented with three different methods, which can be broadly categorized as SDF based methods and Poisson surface reconstruction based methods. Detailed introductions to each method will be provided in the subsequent sections.
SDF based Methods
We employed two SDF-based methods in our exploration, one based on SIREN and the other based on SHINE-Mapping. The input of our system is the sparse point cloud collected from small, low-cost LiDARs, and the output is the smooth dense 3D surfaces.
Mathematic Definition

Pipeline
For SDF-based methods, we first performed Iterative Closest Point (ICP) algorithm to align the point cloud.
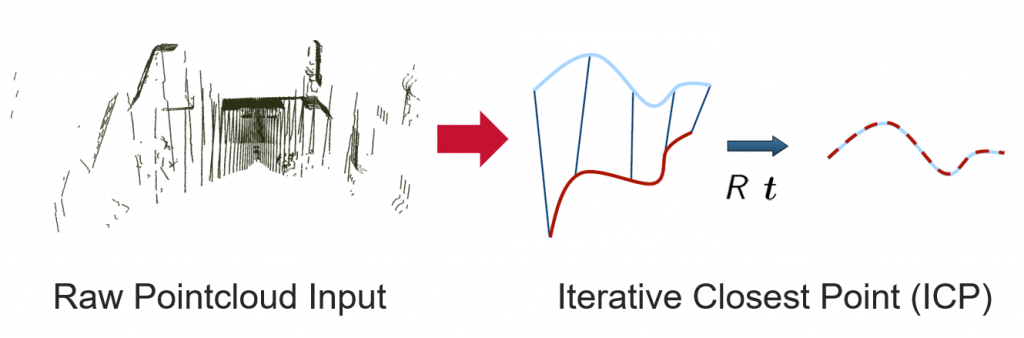
The aligned point cloud is then used as the input of an end-to-end neural network. We used the same loss term for both SIREN [1] and SHINE-Mapping [2], defined as follows:
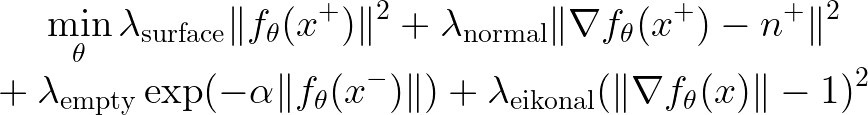
- Surface constraint: for points on surface (+), SDF should be 0. We used the LiDAR intensity information to weight this loss term.
- Normal constraint: for points on surface (+), gradient of SDF should be point’s normal.
- Empty space constraint: for points not on surface (-), SDF should be far from 0
- Eikonal constraint: from differential geometry, SDF gradient’s norm should be 1 everywhere
LiDAR Intensity
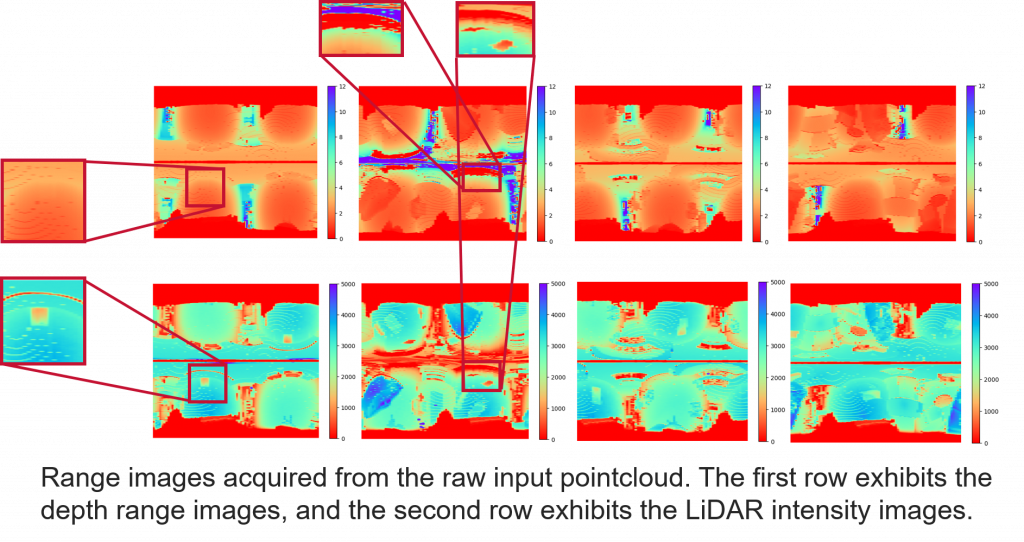
LiDAR intensity is recorded as the return strength of a laser beam, This number varies with the composition of the surface object reflecting the laser beam. The intensity of the laser beam return can also be affected by the angle of arrival (scan angle), range, surface composition, roughness, and moisture content. This means that features under the nadir of the LiDAR sensor usually have higher intensity than the same features along the edges (tilted further), as the returned energy decreases. The strength of the return signal, as well as the reflectivity of the surface, can impact the accuracy of the point cloud. Points with a strong return signal will be more accurate than points with a weak return signal.
However, LiDAR intensity is also greatly influenced by the distance of the point from the sensor. Therefore, we introduced the compensated intensity [3], which is almost independent of depth:
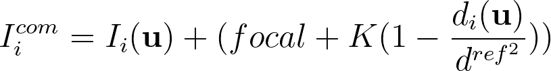
where u is a point in the range image, Ii represents the intensity, di represents the depth, K, focal and dref are the intrinsic parameters of each laser beam after the official calibration. The weight λsurface is then defined as
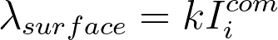
where k is a constant.
Method 1: SIREN
SIREN proposed to use periodic function as the activation function, and can be used to learn a SDF representation from the point cloud of a scene. We used an multi layer perceptron (MLP) of 8 hidden layers, illustrated in the graph below.

Method 2: SHINE Mapping
SHINE learns and store implicit features through an octree-based, hierarchical structure, which is sparse and extensible. The learned implicit features are then transformed into signed distance values using a shallow neural network that follows constraints similar to those employed in SIREN.
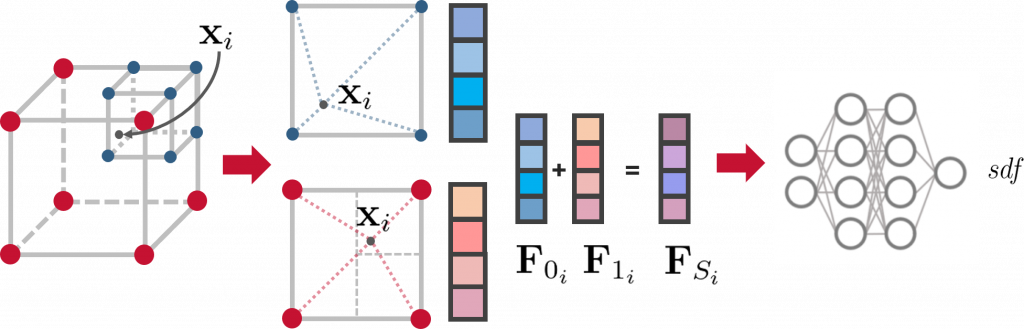
The 3D mesh is then computed from the SDF using the Marching Cubes algorithm [4].
Possion Surface Reconstruction based Methods
Poisson Surface reconstruction
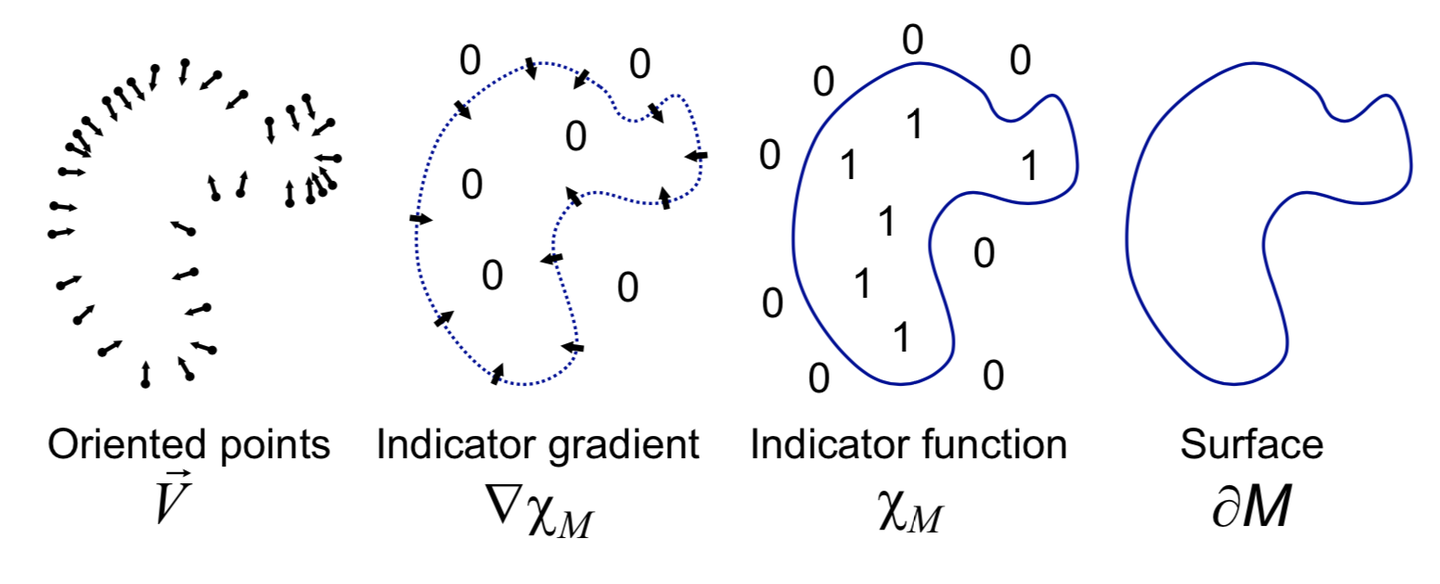
Poisson surface reconstruction [5] is a well known technique for creating watertight surfaces from oriented point samples acquired with 3D range scanners. In this project, we employed Possion reconstruction as the baseline method.
Method 3: Puma
Puma [6] represents the map as a 3D triangle mesh computed via Poisson surface reconstruction. Firstly, the point cloud in the first n frames is aligned using a general ICP algorithm, which is then used to reconstruct an initial mesh representation. In the subsequent frames, the initial reconstruction is combined with the incoming frames using frame-to-mesh registration.
Reference
[1] Implicit Neural Representations with Periodic Activation Functions, NeurIPS 2020
[2] SHINE-Mapping: Large-Scale 3D Mapping Using Sparse Hierarchical Implicit Neural Representations, ICRA 2023
[3] LiDAR Intensity Completion: Fully Exploiting the Message from LiDAR Sensors, Sensors, 2022
[4] Marching cubes: A high resolution 3D surface construction algorithm, SIGGRAPH 1987
[5] Poisson Surface Reconstruction, Eurographics 2006
[6] Poisson Surface Reconstruction for LiDAR Odometry and Mapping
