Dataset

Need for Dataset Creation

Different sets of images were provided by Komatsu of underground coal mines, but it had radial distortion present and the intrinsic parameters of the cameras used to capture those images are not available. These intrinsic parameters are required for Pose estimation problem and therefore, those images cannot be used. Thus, a need raised to create a dataset of images which would resemble the images captured in the coal mines of a mostly flat surface and whose intrinsic parameters are known.

After Discussion, we arrived at Following setup:

A set of 3 cameras with known radial distortion and intrinsic parameters are taken and placed 2-3 meters apart from each other. The cameras are placed in from of the Smith hall building and bike racks are placed in front of the wall to provide some depth in the scene and resemble coal mine images. Here are some sample images.

Undistort Images

As evident from the images above, there is presence of radial distortion as well as tangential distortion in the images. Presence of radial distortion creates a bulge in the image and straight lines look curved in the image. In presence of tangential distortion, the vertically straight surface appears to be slanted backwards. This can be better understood with the help of following image

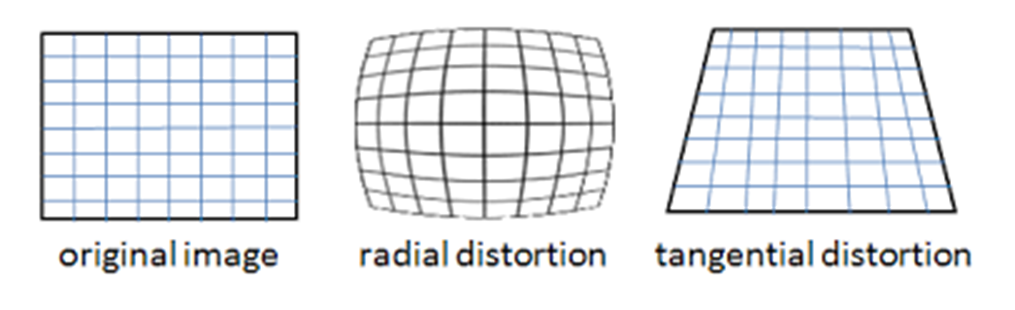
The effects of distortion can be easily modelled using distortion coefficients:

For Radial distortion:
One common model for radial distortion is the “radial polynomial” model, which is expressed as follows:

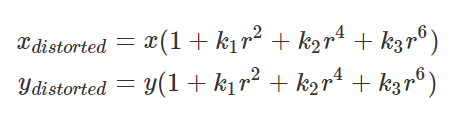
In this equation, x, y are the coordinates of a point in the undistorted image, and x _distorted, y_distorted are the coordinates of the same point in the distorted image. The variable r is the distance from the center of the image, and k₁, k₂, k₃ are constants that describe the amount of distortion.

This model is usually used to correct for radial distortion by finding the values of k₁, k₂, k₃ that minimize the distortion in the image. Once these values have been found, the inverse of the above equation can be used to map points in the distorted image back to their undistorted positions.

For Tangential distortion:
One common model for tangential distortion is the “tangential polynomial” model, which is expressed as follows:

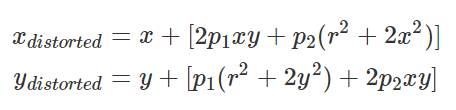
In this equation, x, y are the coordinates of a point in the undistorted image, and x _distorted, y_distorted are the coordinates of the same point in the distorted image. The variable r is the distance from the center of the image, and p₁, p₂ are constants that describe the amount of distortion.

This model is usually used to correct for tangential distortion by finding the values of p₁, p₂ that minimize the distortion in the image. Once these values have been found, the inverse of the above equation can be used to map points in the distorted image back to their undistorted positions..

Results of Distortion Removal