Dataset
The primary reason why Far3Det is not explored is the difficulty in data annotation, i.e., it is hard to label 3D cuboids for far-field objects if they have few or no LiDAR returns. Despite this difficulty, a reliable validation set should be guaranteed for the study of Far3Det. One of our contributions is the derivation of such a validation set, alongside a designed evaluation protocol.
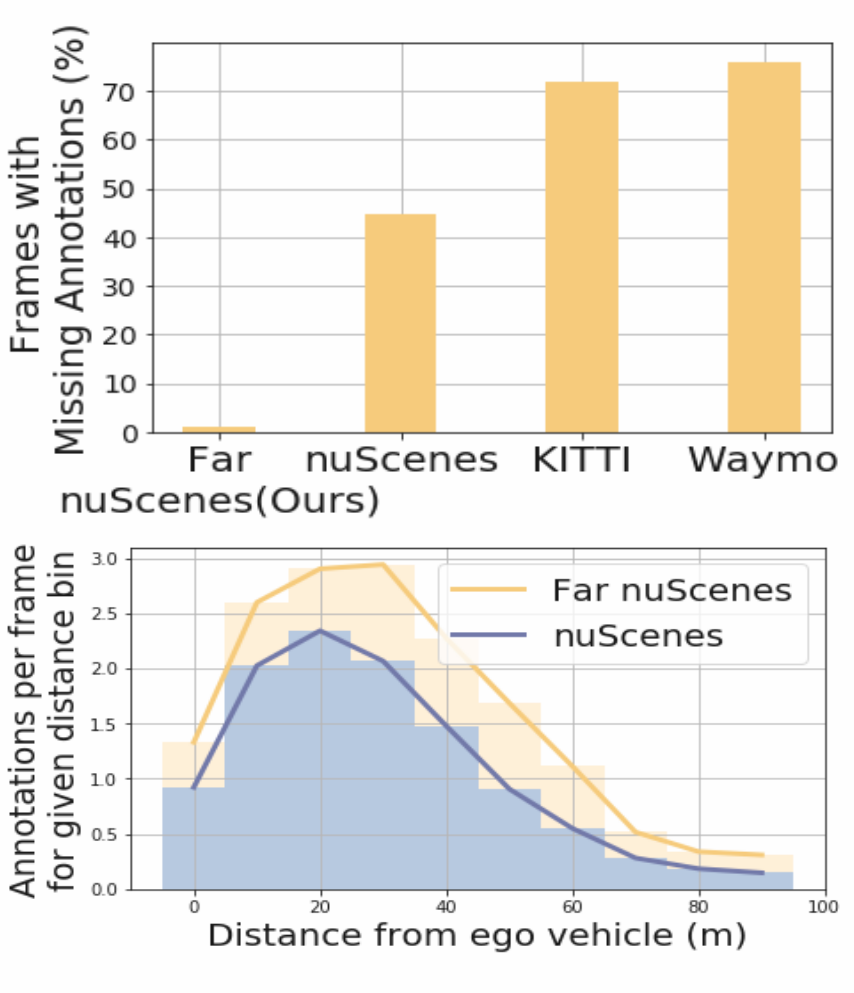
The figure shows ground-truth visualization for some well-established 3D detection datasets. We can see that existing datasets (the first three columns) have significant amount of missing annotations on far-field objects. To obtain a reliable validation set, we describe an efficient verification process for identifying annotators that consistently produce high-quality far-field annotations. This helps us identify high-quality far-field annotations, and derive Far nuScenes (rightmost) that supports far-field detection analysis

Below is the quantitative analysis of the missing annotations for far-field objects in the various datasets. We randomly sample 50 frames from each dataset and manually inspect missing annotations for beyond 50m objects to analyze the annotation quality if existing 3D detection datasets. This analysis suggests that the derived subset Far nuScenes has higher annotation quality compared to existing benchmarks, KITTI, Waymo and nuScenes (b) We compare the average number of annotations per frame at a given distance between Far nuScenes (yellow) over the standard nuScenes (blue), showing that the former (ours) has higher annotation density.
Evaluation Protocol
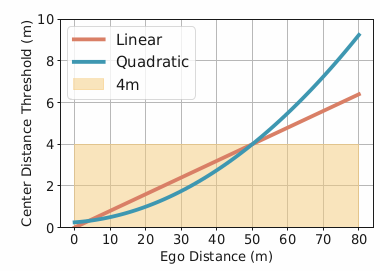
We design two metrics, linear and quadratic as shown below.
The quadratic distance-based threshold can be derived from the standard error analysis of stereo triangulation.
For the linear scheme, we have the threshold given by:
thresh(d) = d/12.5
For the quadratic scheme, we can define the threshold as
thresh(d) = 0.25 + 0.0125d + 0.00125(d2)
where d is the distance from ego-vehicle in meters
While standard metrics count positive detections using a fixed threshold (e.g.,
4m), we design more reasonable metrics with distance-adaptive thresholds. That said, we
adopt thresholds that grow linearly or quadratically w.r.t depth. This imposes not only reasonably relaxed thresholds for far-field objects as humans cannot also perceiving far-field localization, but also stricter thresholds for near-field objects.
Multimodal Sensor Fusion
NMS Fusion
To fuse LiDAR- and image-based detections, we can naively merge them. Under expectation, this will produce multiple detections overlapping with the same ground-truth object. To remove overlapping detections, we apply the well-known Non-Maximum Suppression (NMS). NMS first sorts the 3D bounding boxes w.r.t confidence scores. Then, it repeatedly picks the box with the highest confidence and discards all the boxes overlapping it.
Adaptive NMS (AdaNMS)
We notice that the far-field single modality detections are noisy that produces overlapping detections for the same ground-truth object.
Therefore, to suppress more overlapping detections in the far-field, we propose to use a smaller IoU threshold. To this end, we introduce a distance adaptive IoU threshold for NMS, AdaNMS for short. To compute the adaptive threshold for an arbitrary distance, we qualitatively select two IoU thresholds that work sufficiently well on close range and far-field objects.
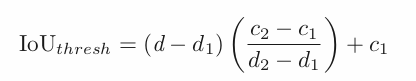
We pick distance ranges d1 = 10m and d2 = 70m and qualitatively select thresholds c1 = 0.2 and c2 = 0.05 respectively.