Motivation

Autonomous driving relies heavily on a detailed vector map. However, constructing a detailed vector map consumes many human and time resources for doing so. The vector map annotated by people is also prone to human mistakes.

Hence, this project explores the state-of-the-art deep learning model to generate the mentioned vector map based on RGB images or spatial coordinates. The dataset used in this project is the Argoverse.

Abstract

We propose Pix2Map, a method for regressing urban street maps from ego-view images. Such technology is a core component of many current self-driving fleets, both for offline map construction and online map maintenance (to accommodate potential changes in street layout due to construction, etc.). This problem is challenging because street maps are often represented as discrete graphs with varying number of lane nodes and edge connectivities, while sensory inputs are continuous arrays of images. We advocate a retrieval perspective, and contrastively learn multimodal embeddings for both ego-view images and graph-structured street maps. We then use these embeddings at test-time to perform cross-modal retrieval; given an ego-view image and its embedding, return the street map (from a training library) with the most similar embedding. We analyze the performance of our method using various graph similarity metrics motivated by urban planning (such as connectivity, density, etc.), and show compelling performance on the Argoverse dataset.

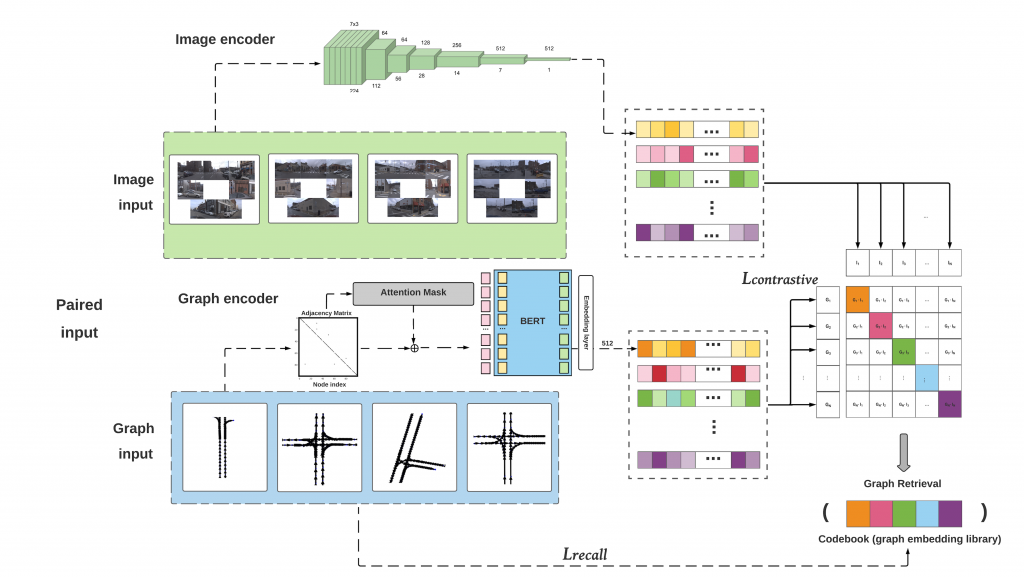
Pix2Map

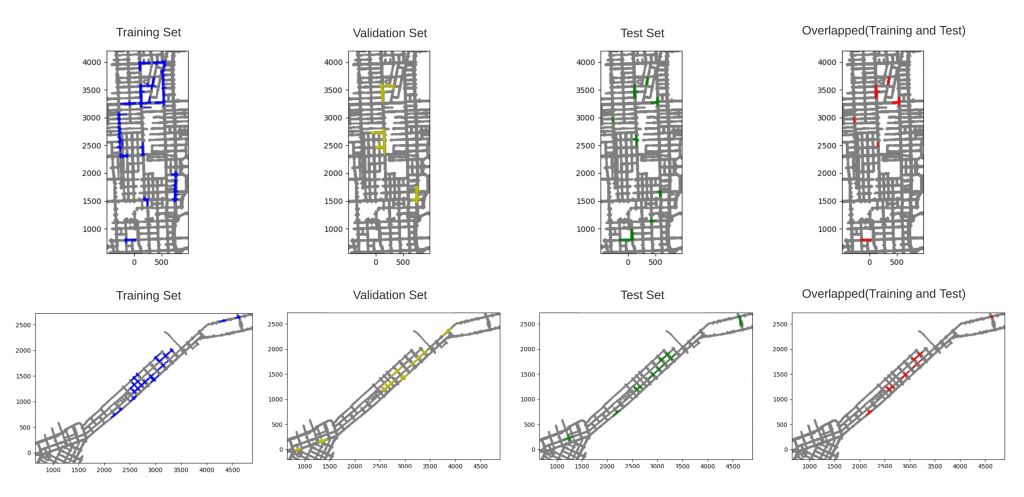
In this work, we advocate a simple formulation of the map construction and map maintenance problem as a visual Pix2Map task: given the ego-view images, generate street maps. Given the recent multi-city autonomous vehicle dataset (Argoverse), it is straightforward to construct pairs of ego-view images and street view maps, both for training and testing. By training and testing on image-graph pairs from different geographic locations (e.g., train on Pittsburgh, test on Miami), one can simulate the map-construction problem. By training and testing on the same geographic location (e.g., train and test on Pittsburgh), one can simulate the map-maintenance problem.

The overall model is shown in below:

Problem formulation

Assume we have a training library of image-graph pairs, written as (I,G) where I is a list of 7 ego-view images from a camera ring and G is an street map represented as a graph G = (V,E), where each vertex v represents a lane node and E represents the connectivity between all lane nodes (adjacency matrix). Importantly, lane nodes are represented with an v = (x,y) position in a local egocentric “birds-eye-view” coordinate frame (such that (0,0) is the ego-vehicle location). Importantly, we allow for different graphs G to have different numbers of lane nodes and connectivity. We use our training library of (image,graph) pairs to learn both an image encoder and graph encoder, as detailed in the following sections.

Image Encoder

Given an image I, we learn an encoder that produces a fixed-dimensional embedding:

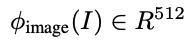
We use a standard image encoder, ResNet18 as a feature extractor by removing its fully connected layer. We experiment with “from-scratch” training as well as with models using ImageNet-pre-trained weights. In order to process the n input images (we use n=7 images throughout our work), we stack them channelwise and then in the pre-trained case replace the first convolution layer with one that stacks the original pre-trained filters n times, with each weight divided by n.

Compared to encode the seven images separately and merge the features, ideally if the model can learn to understand the relationships between the input images, it could better understand what the street layout is. We reuse the original weights when making the new convolutional filters so the benefits of the pretrained weights will be preserved.

Graph encoder

Given a graph G =(V,E), we would like to produce a fixed dimensional embedding:

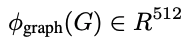
Unlike pixels in an image or words in a sentence, nodes in graphs do not have an inherent order. Hence we would like our graph encoder to be invariant to orderings of graph nodes. To do so, we construct a graph encoder using a transformer architecture defined on lane-graph nodes, inspired by sequence-to-sequence architectures from language that process sequences containing tokens. We treat lane nodes as a collection of tokens and edges as masks for attentional processing.

We encode each input vertex v as 2k-dimensional input embedding obtained by rasterizing its k polyline coordinates. These embeddings are fed into a transformer that computes new embeddings by taking an attentional-weighted average of embeddings from adjacent lane segments. Importantly, we make use of the adjacency matrix E to mask the attentional weighting. We apply M=7 transformer layers, structured similarly to BERT but without positional embeddings. We finally average (or mean pool) all output embeddings to produce a final fixed-dimensional embedding for graph G, regardless of the number of lane segments or their connectivity. In the supplement, we ablate various design choices for our graph encoder.

Image-graph contrastive learning

We use the cross-modal contrastive formalism, but describe it here for completeness. Given N image-graph pairs (I,G) within a batch, our model jointly learns the two encoders mentioned above such that the cosine similarity of the N correct image-graph pairs will be high and and the N^(2-N) incorrect pairs will be low, making use of a symmetric cross entropy loss.

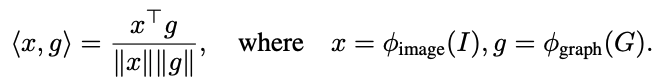
We then compute bidirectional contrastive losses composed of an image-to-graph loss and graph-to-image loss which has the same form as the InfoNCE loss:

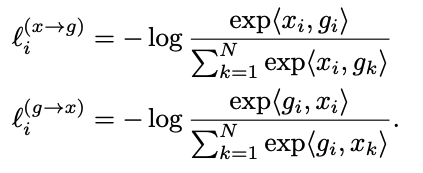
Our final training loss is then computed as a weighted combination of the two losses averaged over all positive image-graph pairs in each minibatch:

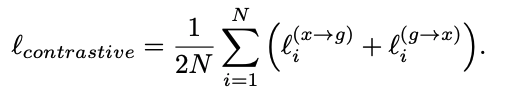
The above penalizes all incorrect image-graph pairs equally. We found it beneficial to (slightly) prefer incorrect matches with similar graphs. Intuitively, we measure the similarity of graph topologies after aligning vertices. Formally, given a ground truth graph G1 and candidate match G2, first establish a correspondence between each vertex v1 and its closest match v2 (in terms of euclidean distances of lane centroids). Given such corresponding vertices, compute a binary cross-entropy loss between adjacency matrix E1 and the permuted matrix E2.

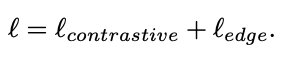
Once the model is trained, we will perform image retrieval and the results are shown in the next section.

Results

Results show that our model succeed in retrieving the graphs using the sensor RGB images, and hence we believe that this is a keystone for generating the vector map automatically. This work is also submitted to the CVPR 2021.