The Epipolar Transformer

Abstract

A common way to localize 3D human joints in asynchronized and calibrated multi-view setup is a two-step process: (1) apply a 2D detector separately on each view to localize joints in 2D, (2) robust triangulation on 2Ddetections from each view to acquire the 3D joint locations. However, in step 1, the 2D detector is constrained to solve challenging cases that could be better resolved in 3D, such as occlusions and oblique viewing angles, purely in 2D without leveraging any 3D information. Therefore, we propose the differentiable “epipolar transformer”, which empowers the 2D detector to leverage 3D-aware features to improve 2D pose estimation. The intuition is: given a 2D location p in the reference view, we would like to first find its corresponding point p′in the source view, then combine the features atp′with the features at p, thus leading to a more 3D-aware feature at p. Inspired by stereo matching, the epipolar transformer leverages epipolar constraints and feature matching to approximate the features atp′. The key advantages of the epipolar transformer are: (1) it has minimal learnable parameters,(2) it can be easily plugged into existing networks, moreover(3) it is interpretable, i.e., we can analyze the locationp′to understand whether matching over the epipolar line was successful. Experiments on InterHand andHuman3.6M [3] show that our approach has consistent improvements over the baselines. Specifically, in the condition where no external data is used, our Human3.6M model trained with ResNet-50 backbone and image size256×256 outperforms state-of-the-art by a large margin and achieves MPJPE26.9 mm.

Method

There are two main components to our epipolar transformer: the epipolar sampler and the feature fusion module. Given a point p in the reference view, the epipolar sampler will, in the source view, compute the locations along the epipolar line from which to sample features. The feature fusion module will then take all the features at the sampled locations in the source view and the feature at p in the reference view, to produce a final 3D-aware feature. We now detail each component, and also some implementation details on how to handle image transformations when using the epipolar transformer.

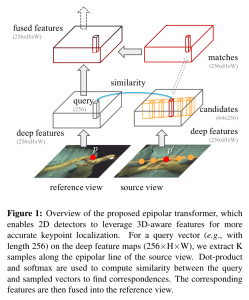
The Epipolar Sampler

We first define the notations used to describe the epipolar sampler. Given two images captured at the same time but from different views, namely, reference view and source view I', we denote their projection matrices as M, M′∈R^{3×4} and camera centers as C, C′∈R^4 in the homogeneous coordinates respectively. As illustrated in figure 1, assuming the camera centers do not overlap, the epipolar line corresponding to a given query pixel p= (x, y, 1) ; in I can be deterministically located on I′.

where M^+ is the pseudo inverse of M, and[·]× represents the skew-symmetric matrix.p’s correspondence p' should lie on the epipolar line, i.e., l^Tp′= 0. The epipolar sampler

S uniformly samples K locations(e.g., 64) on the epipolar linel of the source view, thus forming a set P' of cardinality K. The function takes as input the query location p on the reference view, and the projection matrices M, M'as shown below.

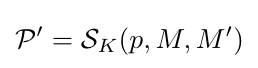
For query points whose epipolar line does not intersect with the source view image plane, we simply skip them.

Feature Fusion Module

Ideally, if we knew the ground-truthp' in the source view that corresponds to p in the reference view, then all we need to do is sample the feature at p': F_source(p′), and then combine it with the feature atp: F_reference(p). However, we do not know the correct p':. Therefore, inspired by Transformer[1] and non-local network[2], we approximateF_source(p′) by a weighted sum of all the features along the epipolar line as follows:

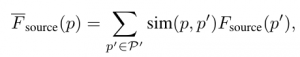
where the pairwise function sim(·,·) computes the similarity score between two vectors. More specifically, itis the dot-product followed by softmax. Once we have the feature from the source view: F_source(p), we can fuse it with the feature in the reference view: F_reference(p) as follows.

Note that the output F_fused is of the same shape as the input F_reference, thus this property enables us to insert the epipolar transformer module into different stages of many existing networks. The weights W_z can be as simple as a 1×1 convolution. In this case, keeping a copy of the original F_reference feature is similar to the design of the residual block.

Experiments

Evaluation metric

To estimate the accuracy of 3D pose prediction, we adopt the MPJPE (Mean Per Joint PositionError) metric. It is one of the most popular evaluation metrics, which is referred to as Protocol#1 in [7]. Itis calculated by the average of the L2 distance between the ground-truth and predictions of each joint.

InterHand Dataset

InterHand is an internal hand dataset that is captured in a synchronized multi-view studio with 80 cameras. 26 unique subjects were asked to do different single and double hand poses in the studio. 7,156 and 1,880 unique single and double 3D hand poses were annotated respectively, which led to 698,922 annotated 2D hands when we projected the 3D annotations to all 80 2D views. For each hand, 21 keypoints were annotated, and therefore there are 42 unique points for two hands.

Experiment setup

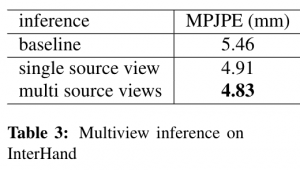
We trained an 1-stage hourglass network [8] with the epipolar transformer included. To predict the 3D joints locations, we run the 2D detector trained with the epipolar transformer on all the views, and then perform triangulation with RANSAC to get the final3D joint locations. During prediction time, our 2D detector requires features from the source view, which is randomly selected from the pool of cameras that were used as the source view during training. We down-sampled the images to resolution 512×336 for training and testing, and only use the RGB images from the 34 cameras for our experiments.

Results

During testing, we can choose different neighboring views as the source view and select the prediction with the highest confidence (i.e., highest Gaussian peak on a heatmap). Shown in Table 3, we test ten views and selected the prediction with the highest confidence for each individual joint. Testing with multi-views reduces the error by 0.1 mm, which is limited.

Visualization

We visualize the results of feature-matching along the epipolar line for both RGB features and the features learned through the epipolar the transformer as shown in Figure 3. It is expected that RGB feature matching will be less robust as different fingers have similar colors, thus leading to high matching scores for all fingers. On the other hand, our deep features trained through the epipolar transformer have the highest matching score when matched against the correct finger, i.e., the deep features are able to discriminate the correct finger from all the other similar looking fingers.

More visualizations and results can be found in the Video demonstration tab.

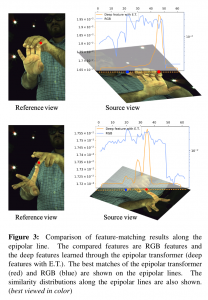
Human3.6M Dataset

Human3.6M [3] is one of the largest 3D human pose benchmarks captured with four cameras and have 3.6M 3D annotations available. The cameras are located at the corners of a rectangular room and therefore have larger baselines. This leads to a major difference compared to the InterHand– the viewing angle difference between the cameras in Human3.6M[3] is significantly larger compared to InterHand.

Experiment setup

As there are only four views in Human3.6M [3], we choose the closest view as source view. We adopt ResNet-50 with image resolution 256×256 proposed in simple baselines for human pose estimation [5] as our backbone network. We use the ImageNet [4] pre-trained model for initialization. The networks are trained for 20 epochs with batch size 16 and Adam optimizer. Learning rate decays at 10 and 15 epochs.

Results

Our epipolar transformer outperforms the state-of-the-art by a large margin. Specifically, using triangulation for estimating 3D human poses, epipolar transformer achieves 33.1 mm, which is ∼12mm better than the cross-view [6], using the same backbone network(ResNet-50, input size 256×256). Using the recursive pictorial structural model(RPSM [6]) for estimating 3D poses, our epipolar transformer achieves 26.9 mm, which is ∼14mm better than cross-view [6]. More importantly, epipolar transformer on ResNet-50 input size256×256 even surpasses the state-of-the-art result from cross-view [6] on ResNet-152 input size 320×320 by∼4 mm, which is 13% relative improvement. We argue that epipolar transformer finds correspondences and fuse features based on feature similarity, which is superior to cross-view [6] which uses fixed attention for specific camera settings. Our model with data augmentation achieves MPJPE 30.4mm with triangulation, which is better than state-of-the-art even without RPSM.

Visualization

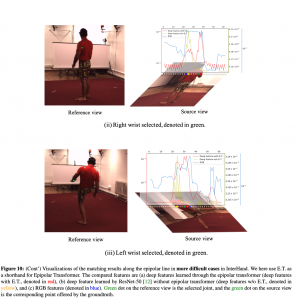
More visualizations and results can be found in the Video demonstration tab.

Reference

[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems , pages 5998–6008, 2017.

[2] Xiaolong Wang, Ross Girshick, Abhinav Gupta, and Kaiming He. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 7794–7803, 2018

[3] Catalin Ionescu, Dragos Papava, Vlad Olaru, and Cristian Sminchisescu. Human3. 6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE transactions on pattern analysis and machine intelligence, 36(7):1325–1339, 2013.

[4] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference, pages 248–255. IEEE, 2009.

[5] Bin Xiao, Haiping Wu, and Yichen Wei. Simple baselines for human pose estimation and tracking. In Proceedings of the European Conference on Computer Vision (ECCV)

[6] Haibo Qiu, Chunyu Wang, Jingdong Wang, Naiyan Wang, and Wenjun Zeng. Cross view fusion for 3d human pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, pages 4342–4351, 2019.

[7] Julieta Martinez, Rayat Hossain, Javier Romero, and James JLittle.A simple yet effective baseline for 3d humanpose estimation. InProceedings of the IEEE InternationalConference on Computer Vision, pages 2640–2649, 2017.

[8] Alejandro Newell, Kaiyu Yang, and Jia Deng.Stacked hourglass networks for human pose estimation. In European conference on computer vision, pages 483–499. Springer,2016